1954 Geometria 264

nice vpisanej do w-uholnika. Uhol pri hlavnom vrchole każdeho z tychto trojuholnikov rovna sa

PR

n

V tej to kapitole si vśimneme, ako zavisi vel’kost strany a_n a obsah pravidelneho w-uholnika od polomeru opisanej a ypisanej krużnice.

Ul oh a 1. Urcte stranu a_n pravidelneho w-uholnika ypisaneho do danej krużnice.

Riesenie. Nech je dana krużnica k o polomere r a strede 0 (obr. 19). Strana hladaneho w-uholnika je AB = a_n. Trojuholnik¹) [\ABO je roynoramenny, preto os OP strany AB je osou uhla <j:AOB =

= —. Teda

n

<£AOP= <£BOP = —.

w

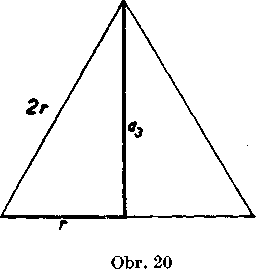
Z prayouhleho trojuholnika A -dOPdostaneme

l

. 2 B    2^a™

sin — = ->

n    r

także

a_n

_n . 2B = 2r. sin —.

n

(1)

Tym sme odvodili yelkost strany a_n pravidelneho w-uholnika vpi-saneho do krużnice o polomere r pre lubomlne n A 3. Na priklade ukażeme konśtrukciu pre n = 3, t. j. zostrojime stranu pravidelneho (rovnostranneho) trojuholnika ypisaneho do danej krużnice. Yzorec (1) pre n — 3 ma tvar

„    . 2E

= 2r. sm ——,

3    3

ciże

a₃ — 2r. sin 60°.

Pretoże sin 60° = — ]/3, je

u

a₃ = r.y 3.

Konśtrukcia je znazornena na obr. 20.

01 o h a 2. Urćte stranu a_n pracidelneho w-uholnika opisaneho danej krużnici.

Riesenie. Nech je dana krużnica k o strede 0 a polomere o (obr. 21). Strana hladaneho w-uholnika je AB = a_n. Trojuholnik /\ABO

4 R

je rovnoramenny, jeho vyśka o je sucasne osou uhla AAOB = —.

V priklade si ukażeme konśtrukciu pre n = 6, t. j. zostrojime pravi-delny śesfuholnik opisany danej krużnici.

Pre n = 6 ma vzorec (2) tvar

2 R

= ²e-tg

ćiźe

a₆ = 2g.tg 30°.

1

Kedże predpokladame n A 3, uhol <£AOB = — je duty. Tento uhol

móże by6 teda vnutornym uhlom trojuholnika, także ABO je skutocne trojuholnik.