1954 Geometria 130

jeden z nich previes< prenriestenim (zhodnoslou) do utcaru róvnó-1’ahleho s druhym.

Poznamky

1.    Pretoże aj totożnosf povażujeme za zhodnosf , su każde dva rovno-l’ahle utvary podobne.

2.    Każde dya zhodne utyary możno premiestenim stotożnit alebo previest do utvarov stredove sumernych. Ako vieme, je stredova su-mernost roynolahlosfou; preto su każde dva zhodne utyary podobne.

A--—H-

C    B    A

Obr. 149

Priklad 11. Mamę dokazat tieto tyrdenia:

Każde dve usecky su podobne. Każde dve priamky su podobne. Każde dve krużnice su podobne. Każde dva śtvorce su podobne.

Dva uhly (dute) su podobne iba vtedy, ak su zhodne.

/

Obr. 150

stredu A; koeficient roynolahlosti

Riesenie. a) Usecky premies-time do takej polohy, aby mali spolocny krajny bod a aby.prislu-chali opacnym polpriamkam (AB a BC na obr. 149). Potom rovno-1’ahlosf so stredomR, która preva-dza bod A do bodu O, prevedie useeku AB do usecky BC.

b)    Tvrdenie o priamkach vyply-va z predchadzajucej poznamky 2.

c)    Tvrdenie o krużniciach bolo dokazane vo yete 2.

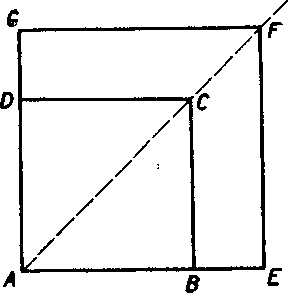
d)    Stvorce (ak nie su zhodne) pre-miestime tak, ako znazorńuje obr. 150. Stvorec ABCD je potom rov-nolahly so śtyorcom AEFC podia . AB

^]e AE'

e) Ak su uhly tx, a' podobni, możno podia definicie podobnych utvarov zostrojit uhol oc" zhodny s a' tak, że    su rovnol’ahle.

Każde dva rovnol’ahle uhly su vśak zhodne (pozri vety na konci clan-ku 1). Je teda

x" = x', x" = oc,

preto x = <%'.

V algebre sme poznali krivky, zvane paraboly.

Priklad 12. Mamę dokazat, że każde dve paraboly su podobne.

/

Riesenie. Paraboly sme zaviedłi pri znazor-novani funkcii ako grafy kvadratickej funkcie. Vhodnym premiestenim dvoch parabol móżeme dosiahnut, że su grafmi funkcii

(1)    y .= ax²,

(2)    y = bx\

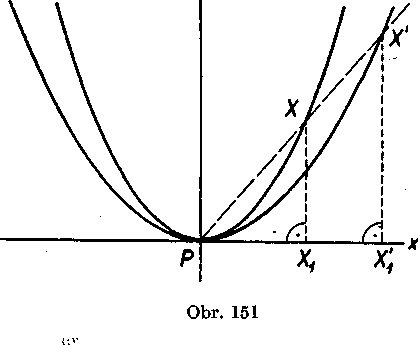
kde a, b su kladne cisła (obr. 151).

Ak je a = b, su paraboly totożne,t. j. zhodne, t. j. aj podobne. Ak je a ^ b, zavedieme rovno-lahlosf, która ma stred v zaciatku P suradnic

a która ma koeficient Parabola (1) je mnożina bodov so surad-nicami (x; ax²), kde x nadobuda vsetky realne hodnoty.

Oznacme X₁ bod (na osi x) so suradnicami (x\ *0), X bod so surad-nicami (x; ax²). Ak je x ^ 0, prevedie rovnoIahlosf so zaciatkom P

a s koeficientom ~~ trojuhołnik PXX₁ do trojuholnika PX'X\\

⁰    i

bod X₁' budę maf suradnice (—x; 0), bod X' budę mat suradnice

f    U/    /    w    n    ^91

x = — x, y =— ax^z = ■— x^l = b.

b²‘

b.X'².

Preto bod X' prislucha parabole (2).

131