1954 Geometria 268

II. OBSAH KRUILU A DŁZKA KRUŻNICE

1. Obsah kruhu a jeho casli

Ked’ sme sa v śiestej tTTUtte zauberałi ubSShmi oBrazcov, stretli sme sa nielen s obsahmi mnohouholnikov, ale aj s obsahom kruhu. Pritom pre Yypocet obsahu kruhu sme poużivali tuto vetu:

Obsah kruhu o polomere r rovna sa P = nr'², kde n = 3,14.

Najprv muslme presne definovafi, co rozumieme pod pojmom obsah kruhu. Pojem obsahu sme si totiż definovali len pre mnohouholniky a kruh nemożno rozlożit na konecny pocet trojubolnikov.

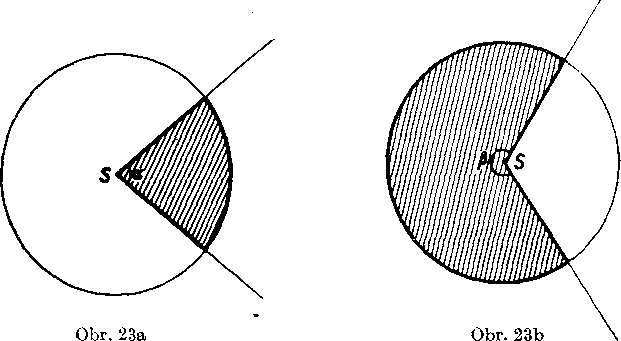
Rozślrime teraz pojem obsahu tak, aby do teraj śl pojem obsahu (t. j. obsah mnohouholnlka) a obsah kruhu boli len jeho osobitne pri-pady. Tento pojem obsahu rozślrime aj pre śirśiu skupinu obrazcov.

Najprv presne vymedzime, pre które obrazce budeme definovat obsah.

V predoślych kapitolach sme poznali, że kruh o polomere r a strede S je mnożina bodov, które sa skladaju zo vsetkych bodov krużnice o polomere r a strede S a zo vsetkych bodov nachadzajucich sa vo vnut-ri tej to krużnice. Okrem toho budeme sa zaoberat tymi to castami kruhu: Je to jednak

kruhovi) vysek (obr. 23ab). Kruhovy yysek je mnożina bodoy spo-locnych kruhu a uhlu, ktoreho vrchol je v strede S tohto kruhu. Na obr. 23a je narysoyany yysek, ktoreho uhol oc je duty. Uhol /? yyseku na obr. 23b je yypukly.

Inou castou kruhu je

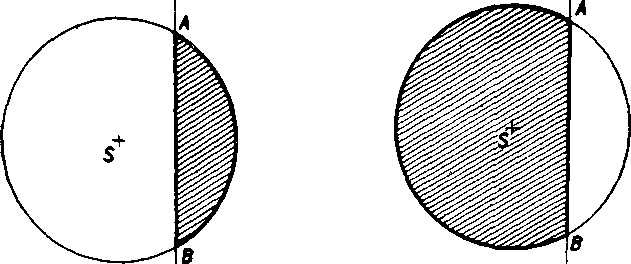
kruhovy odsek (obr. 24a, b) . Je to mnożina bodov spolocnych kruhu a jednej z polroyin, których hranićnou priamkou je secna AB pri-sluśnej krużnice.

Obr. 24a

Obr. 24b

Poznamka. Polkruh móżeme povażovat bud za vysek, ktoreho uhol je 2B, bud za taky odsek, kde priamka AB prechadza stredom 8 krużnice.

Mnohouholniky, kruh, kruhovy yysek a odsek nazveme zakladnymi obrazeami.

Okrem tychto obrazcoy budeme sa zaoberaf aj utvarmi:

1.    które yzniknu zlożenim neprekryvajucich sa zakladnych obraz-cov. Take su napr. utvary na obr. 25;

2.    z których po doplneni zakladnymi obrazeami yzniknu ine za-kladne obrazce. Vyżadujeme pritom, aby vzniknuty zakladny obrazec bolo możne rozlożit na neprekryyajuce sa utvary, z których jeden je prave dany utvar a każdy zyyśujuci je zakladny obrazec. Takymto utvarom je napr. vyśrafovana casf kruhu na obr. 26. Tento utvar doplnime na kruh trojuholnikom T, odsekom U a kruhom K. Iny pri-

269