1954 Geometria 304

Toto staći dokazat len pre kosę hranoly, lebo y prlpade kolmych hranoloY sa tvrdenie zhoduje s tvrdenim vety 1. Pre prehladnost dokażeme płatu ost’ len pre kosy patboky hranol ABGEDA'B'0'D'E', który nazveme Hj (obr. 60). Najprv zostrojime hranolovy priestor pri-sluśny danemu hranolu, t. j. ćast priestoru yyplnenu priamkami rovno-

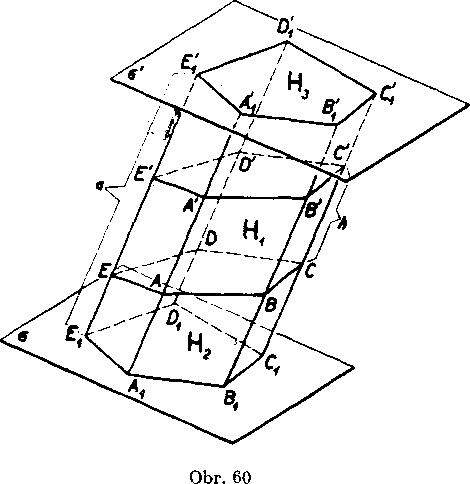
beżnymi s bocnou hranou AA', które pretinaju patuholnik ABC DE. I)alej zvolime dve roviny a a a' kolme na hrany hranoloveho priestoru tak, aby z neho yytlnali koimy hranol    [B[C{D[E[,

który by ako cast obsahoval dany kosy hranol; oznacme ho H.

Zostrojeny hranol możno rozlożit na tri navzajom sa neprenikajuce telesa; jednak na dany hranol H₂ a jednak na mnohosteny A₁B₁C₁D₁E₁ ABCDE a A'B'C’D'E'A{B[CID{E[, które nazveme H₂ a H₃.

Z ylastnosti [3] (str. 295) vidno, że objem hranola H₁ najdeme, ked od objemu hranola H odpocitame sucet objemov mnohostenov H₂, H₃.

Objem hranola H sa rovna an, kde a znaci jeho vyśku a n obsah podstayy. Aj sucet objemov mnohostenov H₂, H₃1’ahko urćime. Podia ylastnosti [3] (str. 295) sa tento sucet rovna objemu kolmeho hranola, który dostaneme, ked z hranola H yyjmeme dany hranol H₁ a posu-nieme H₂ a H₃ v smere hran hranoloyej płochy tak, aby patuholniky

ABODE a A'B'C'D’E' splynuli. Ak hrana daneho hranola je h, vyska hranola zostrojeneho z mnohostenoy H_a a H₃ je a — h, rovna sa jeho objem (a — h) n.

Objem daneho koseho hranola H_x sa teda rovna an — (a — h)n = hn, t. j. rovna sa sucinu vel'kosti hrany a obsahu podstavy A₁B₁C₁D₁E_V Tato podstava je vśak kolmym rezom hranolovej płochy. Ak uvażime, że vsetky kolme prierezy tejto płochy su zhodne mnohonholniky, vetu sme tym dokazali.

Teraz uż móżerne odvodit zakladnu vetu pre ureenie objemu Iubo-vo!neho hranola.

Yeta 3. Objem hranola rovna sa sucinu obsahu podstavy a vel’kosti vy§ky.

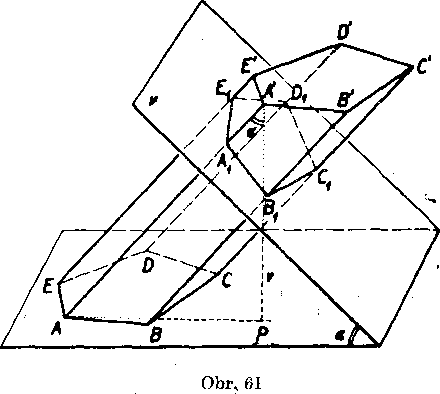
Dókaz. Tuto vctu sme uż dokazali pre kolme hranoly, zostava dokazat ju eśte pre kosę hranoly. Ne eh je dany kosy patbolcy hranol ABCDEA'B'G'D'E'-, plsmenom a oznacme odchylku roviny y 1’ubo-Yolneho kolmeho rezu A₁B₁C₁D₁E₁ hranolovej płochy prlslusnej danemu hranolu od roviny jeho podstayy (obr. 61).

Ak obsah kolmeho rezu daneho hranola je n a dtżka jeho bocnej hrany h, potom podia predoslej pomocnej vety objem hranola rovna sa nh.

Koimy rez A₁B₁0₁D₁E₁ je vsak pravouhlym priemetom podstavy ABCDE (a rovnakej podstavy A'B'0'D'E') daneho hranola do royiny,

305