1954 Geometria 138

S axiómami I a II sme śa oboznamili uż v 6. rocniku. Vieme, że yysloyuju matematicky velmi jedncduche skusenosti: Axiómu I si znazornime napr. napnutim śnury medzi dvoma kolikmi, axiómu II prikladanim priamej hrany lineara k rovnej doske.

Axiómy III, IV su pre nas nove, ale urćite budeme ochotne bez rozpakov verit ich spravnosti. Su totiż prave tak ako ysetky ostatne axiómy odvodene z hmotneho sveta około nas. Ich spravnost nam zarucuje mnohokrat overeny suhlas so skusenostou, s pozorovanim. Ak si napr. predstavime rovinu znazornenu otyorenymi dvermi, móże-me povażovaf, tu ich hranu, na której su pripevnene panty, za znazor-nenie priamky p. Touto priamkou p nie je poloha dvier jednoznacne urcena, pretoże dvere móżu zaberat pri otvarani a zatvarani nekonecne mnoho polóh a ich rovina pri tom stale obsahuje priamku p. Ak vśak zvollme mimo priamky p nejaky bod, napr. gumovu zarazku na dlaż-ke, je iba jedina poloha dvier, ked’ sa dotykaju zarażky. Toto je obraz hmotneho sveta, który odpoveda tvrdeniu axiómy III. Tak isto możno najst velke mnożstvo prikladov na axiómu IV. Napr.: Dlażka a prie-celna stena ucebne maju spolocny bod — napriklad jeden z prednych dolnych fohov ucebne — potom maju spolocnu celu hranu, v której sa stykaju a nijake ine body.

Vo vsetkych śtyroch axiómach I aż IV yyskytuj u sa vyroky: „bod leż! na priamke, priamka prechadza bodom, rovina obsahuje bod, dve roviny maju spolocnu priamku¹¹ a pod. Vśetky tieto vyroky zname-naju polohove vzfiahy, które możno vyjadrit pomocou jedineho slova „incidoyat¹¹ (byt incidentny). (Incido z lat. — padam na nieco.) Tak napr. vyrok „bod A a rovina q su incidentne¹¹, znamena presne to iste ako vyroky: „bod A leżi v rovine o“ alebo „royina r> obsahuje bod A“ alebo ,,rovina p prechadza bodom A“ a pod. Axiómy I aż IV na-zyvame strucne axiómy incidencie.

Prave tak ako v planimetrii aj v stereometrii si pic Lstayujerne, że geometricke utvary su zlożene z bodov. Priamka alebo rovina je mno-żina yśetkych bodov, .które s ńou inciduju. Vyrok „priamka p leżi v rovine q“ znamena, że każdy bod priamky p. t. j. każdy bod, który leżi na priamke p, leżi aj v rovine q.

Pomocou axióm I aż IV możno dokazat dve jednoduche vety.

Veta 1. Troma bodmi, które neleżia na jednej priamke, prechadza jedinti rovina.

Dókaz. Dane body oznacme A, B, G. Body A, B su różne, pretoże keby splynuli, leżali by body ApB, C na jednej pridmke. Obidvoma bodmi A, B prechadza podia axiómy I jedina priamka p; bod C na tejto priąryikc neleżi. Rovina, która ma prechadza! bodmi A, B, C, musi obsahovat podia axiómy II aj priamku p; bodom G a priamkou p prechadza vsak podia axiómy III jedina rovina. Tym je yeta 1 doka-zana.

Rovinu prechadzajucu troma bodmi A, B, C budeme oznacovat g ss ABC.

Veta 2. Dvoma r6znymi priamkami, które maju spoloCny bod, pre-ch&dza jedina ronina.

Dókaz vety 2 je obdobny dókazu vety 1; vetu vsak nebudeme do-kazovat.

Rovinu g obsahujucu dve różne priamky p, q, które maju jediny spolocny bod, zapisujeme g = pq.

Vety 1 a 2 su velmi nazorne, rozhodne o nic menej ako same axiómy. Uvedieme teraz ako priklad yetu menej nazornu, pri której sme o spravnosti pevne presvedceni prave iba preto, że yyplynula uvahou z axióm, pripadne z yiet, które boli odyodene na zaklade axióm.

Priklad 1. Je dane n różnych priamok, z których każde dve sa navzajom pretinaju. Dokażte, że tieto priamky bud' ysetky prechadza-ju jednym bodom, bud’ ysetky leżia v jednej rovine.

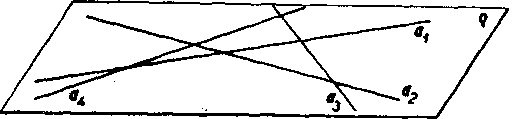
Obr. 1

Riesenie. Oznacme dane priamky a_L, a_%,..., a_n. Ak n == 2, veta je spravna. Oznacme A priesecikpriamok^, a₂ a groyinua₁a_a. Ak n > 2, priamky a_v a₂,..., a_n prechadzaju bud' vsetky bodom A, bud aspoh jedna — oznaćime ju a_s — bodom A neprechadza. Pretoże a_s pretina Oj, ako aj a_a, a to v różnych bodoch, leżia podia axiómy II (obr. 1) ysetky body priamky «_:i v rovine g. Ak jo n > 3, potom każda dalsia priamka a₄,. .., a_n pretina vśetky tri priamky a_v a₂, a_s a z tychto troch priesecikoy su aspoh dva różne, pretoże priamky a_x, a₂, a₃ ne-prechadzaju jednym bodom. Ma teda każda z priamok a₄,..., a_n s ro-vinou g aspoh dwurożne body spolocne, a preto podia axiómy II leżi v royine g.

139