1954 Geometria 110

rovinny utvar. Na to poużijeme zobrazenie, zvarie roYnolahlosf ciże homotetia. Na j skór uvedieme priklad.

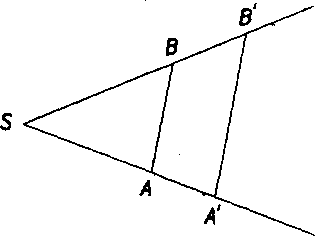
Priklad 1. Na obr. 126 je trojuholnik ABC a bod S, który leżi mimo neho. Na polpriamkach SA, SB, SG su zostrojene po rade body A', B', G', pre które plati

SA'= 2.SA, SB' = 2. SB, SC’= 2.SC.

Marne dokazaf, że plati

A ABC ~ A A’B’C.

Rdesenie. Bod S na obr. 126 neleżi na żiadnej z priamok AB, BC, CA. Vzniknu preto trojuholniky SAB, SBC, SGA a aj trojuholniky SA'B', SB'C', SC A'. Podia vety su o podobnosti trojuholnikoy plati

&SA’B’~ &SAB, ASB'C'~ &SBC, &SCA'~ ASGA.

Z tychto vztahov odyodime rovnosti

A'B' = 2 AB, B'C = 2 BC, CA' = 2 CA, a tym je tvrdenie dokazane.

Na obr. 126 je este bod X, który leżi medzi bodmi A, B, a zostrojeny je bod X' polpriamky SX, pre który plati SX' = 2 SX; bod X' leżi medzi A’, B¹.

Na obr. 126 je d’alej bod Y trojuholnika ABC, który neprislucha jeho obvodu, ciże leżi vo vnutri trojuholnika ABC. Zostrojeny je aj bod 7.' polpriamky SY, pre który plati SY’ — 2 SY; bod Y' leżi vo vnutri trojuholnika A'B'C'.

V priklade 1 sme | j| | SX    poznali spósob, którym

-1-1------ -----------l ■■    - możno zvac§ittrojuhol-

X‘ S    X    nik ABC na trojuhol

nik A'B'C'. Tentospó-Obr. 127    sob możno poużif pri

IubovoInom utvare.

Nech je dany peyny bod S (obr. 127) a realne cislo 1, rozdielne od nuly a jednej. Ku każdemu bodu X roviny zostrojime bod X' takto:

Pre bod X = $ je X' = S. Ak X ^ S, zostrojime bod X’ na priam-ke SX tak, aby pre yelkosf useciek platilo SX' = (AJ.&5T; pritom zostrojime bod X' na polpriamke SX, ak je X > 0, a na polpriamke opaŚnej k SX, ak je X < 0.

Podia tohto pravidla je każdemu bodu X priradeny jediny bod X';

toto priradenie (zobrazenie) vola sa rovnoIahlosf. Bod 8 sa vola stred rovnol’ahiosti, ćislo X koeficient roynolahlosti. Bodu X budeme hovorif — podobne ako pri zhodnosti — vzor, bodu X' obraz. Bod S, który splyva so svojim obrazom, je pre rovnol’ahlosf samodrużny.

Poznamky

■ 1. V priklade 1 bola uyedena rovnoI'ahlosti s koeficientom 2.

2.    Je jasnó, preco vylucujeme cisla X — 0 a X = 1. Keby sme pri-pustili X = 0, boli by obrazy vsetkych bodov v bodę S. Keby sme pri-pustili X = 1, dostali by sme totoznost, ktoru nie je vhodne povażovat za rovnol’ahlost.

3.    Pre X = — 1 je rovnoIahlost stredovou sumernostou.

Ak zostrojime ku vśetkym bodom urćiteho utvaru U ich obrazy v urcitej rovno!ahlosti so stredom S, dostaneme novy utvar UHovo-rime, że utvar U' je obraz utvaru U v danej rovno!ahlosti, alebo że utvar U' je rovnol’ałily k ótvaru U podia stredu 8, alebo że dana rovno-lahlosf prevadza utvar U v utvar U'. Dóleżita je najma veta o utvare roynolahlom k usecke.

SMM'    8    8’

-1 -1-H

—1—-- Obr. 128a S A a! B ^1 ił i	-1- B’ - i
1 i i l
Obr. 128b
X A s	b a'
—l—l-1-	—i-1-

Obr. 128c

Obr. 128d

Veta 1. RoTnorahlosf so stredom 8 a koeficientom X prevadza useCku AB v useCku A’B'. Obidye useCky su navzajom roynobeźne a plati

A'B' = \X\.AB.

Dokaż. TJsecka AB może fnat yzhladom na stred rovnoIahlosti róznupolohu; obr. 128abcdznazorńuju Styri pripady, które treba pre-

111