032

Jako nazorna ilustrace vam muźe poslouźit treba i tento sa-mozrejmy fakt: nasobime-li komplexni Cisło 2, ktere ma argument <f = 0, komplexni jednotkou i, kterama argument a = dostaneme cislo 2i, ktere ma argument = 0 + ^7t = f 4- a.

Nyni je uż videt, że umime-li komplexni Cisla graficky naso-bit Cislem realnym i komplexni jednotkou, uniinie graficky sestro-jit soucin jakychkoli komplexnich Cisel. StaCi si totiż uvedomit, że komplexru Cisło z. kterym nasobime, si mużeme predstavit ve tvaru z = |^|(cos<j? + isinv?), tj. jako soucin realneho Cisla \z\ a komplcxni jednotky cos<£ + isiny>. Nasobeni komplcxnim Cislem je tak preve-deno na nasobeni Cislem realnym a nasobeni komplexni jednotkou, priCemź nezaleźi na tom, zda nasobime nejprve realnym cislem a pak komplexni jednotkou, nebo obracene. IJkaźeme si to na konkretnim pfikladu.

Priklad 15

Graficky urcete soucin (—1 + i)(1 + i).

Reśeni

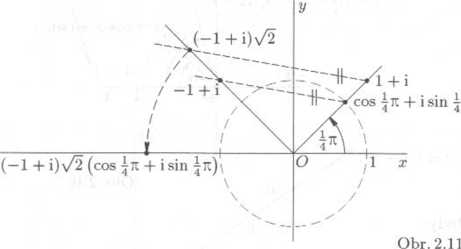
(Viz obr. 2.11.) Cislo 1+i vyjadfime ve tvaru \J2 (cos + i sin ku) a Cislo —1+i vynasobime nejprve Cislem \/2. Protoże cislo (-1 +i)\/2 je obrazem Cisla -1 + i ve stejnolelilosti se stredem v pocatku a s koeficientcm \/2 a protoźe v teze stejnolehlosti je Cislo 1 + i obrazem cisla cos iit + i sin leźi cislo (-l+i)V2 nobCźce vedene bodem 1 + i s primkou urćenou body —1 + i, cos j7c + i sin jK. Zbyva vynasobit cislo (—1 + i)\/2 komplexni jednotkou cos jit + i sin i-it, tj. otocit, je kołem poćatku o uhel Tiiri je soucin (-1 + i)\/2 (cos jtc + i sin jti) = (-1 + i)(l + i) sestrojen. Vypoćtem se muźete pfesvCdcit, źe je (—1 + i)(1 + i) = —2.

na rov-

Pozndrnka. Urćit soućin danych cisel mfiźete take tak, źe sestrojite nejprve cislo (—1 + i) (cos + i sin j 7t) a potom toto cislo yynasobite \/2- Chcete-li, muźete postupovat jeśte jinak: vyjadrit jako soućin realneho cisla a komplexni jednotky cislo —1+i a timto realnym cislem a kornplexni jednotkou postupne nasobit cislo

1+i.

Je zrejme, źe tyto poznatky umoźńuji znazornit graficky i podli komplexnich cisel. Vime totiź, źe delit komplexnim cislem r (cos <p + i sin tp) znamena nasobit Cislem

_1_

r (cos <p + i sin tp)

- [cos(-<?) + i sin(—v?)].

Priklad 16

Graficky urćete podli ^    .

Reśeni

Prevedenim podilu na souCin dostaneme

-1+i _    -1+i    _

1 + i \/2 (cos jTi + i sin jTt)

= (-¹ +i)^| [cos(-H+isin(-H] •

Podle obr.2.12 sestrojime nejprve soucin

(-1+i) [cos (—+ i sin (— 4^7T)] 5

63