1011

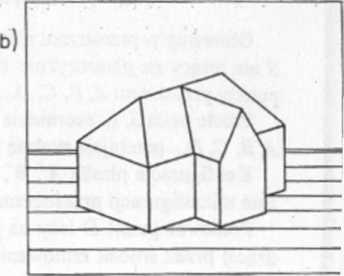
Rys. 5

Rzut równoległy umożliwia konstrukcją obrazu aksonometrycznego, np. wie lościanu, dając obraz podobny do wrażeń wzrokowych podczas obserwacji mo delu wielościanu ze znacznej odległości (rys. 5b).

1.3J. Rzut równoległy prostokątny według metody Monge’a

Półosie dodatnie kartezjańskiego układu współrzędnych wyznaczają param płaszczyzny - rzutnie (rys.6a): x i y rzutnia pozioma 7T,, x i z rzutnia pionowa n_v y i z rzutnia boczna n_y

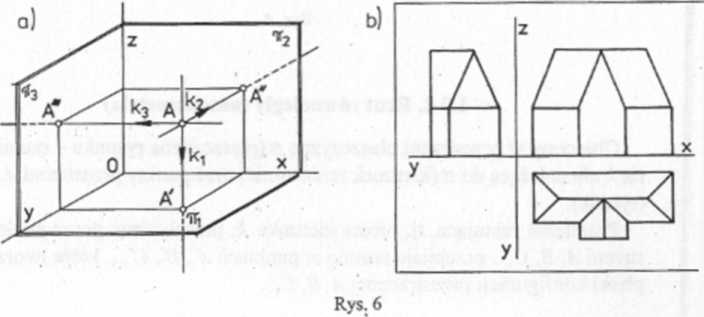
Promienie rzutujące tworzą wiązki równoległe, które przechodzą przez punkty A, B, C, D,... przestrzeni i przebijają kolejno rzutnie it_v 7^.

Tworzymy zatem 3 wiązki prostych rzutujących, które są prostopadłe kolejno do rzutni:

7T, - kierunek rzutowania k_{ || do osi z,

7i_l - kierunek rzutowania    || do osi y,

71j - kierunek rzutowania k₃1| do osi x.

Otrzymujemy więc 3 rzuty równoległe prostokątne, np. wielościanu (rys. 6b), jako widok z góry, z przodu i z boku danego wielościanu, na tle rzutni poziomej, pionowej i bocznej.

Obraz w rzucie środkowym (perspektywa) ma przede wszystkim charakter poglądowy przy utrudnionym odtwarzaniu wymiarów danego obiektu (szerokość, głębokość, wysokość).

Obraz w rzucie równoległym (aksonometria) przy pewnych założeniach formalnych jest jednocześnie rysunkiem poglądowym i miarowym.

Obraz w rzucie równoległym prostokątnym według metody Monge’a jest natomiast przede wszystkim rysunkiem miarowym, stąd jego powszechne zastosowanie w technice jako zapis. Stwarza jednak pewne trudności w odczycie dla osób nieprzygotowanych.

Pomijając rzut środkowy, jako mało przydatny w technice, spróbujmy prześledzić podstawowe elementy geometryczne i ich relacje, odwzorowane początkowo w rzucie równoległym (aksonometria), posiadającym jednocześnie charakter rysunku poglądowego i miarowego.

1.3.4. Rzut równoległy (aksonometria)

Obierzmy na płaszczyźnie rysunku dwie półosic dodatnie x i z kartezjańskie-go układu współrzędnych jako wzajemnie prostopadłe oraz półoś y pod kątem 45° w stosunku do osi x. Na osiach x i z odłóżmy odcinek jednostkowy o jednakowej długości, na osi y natomiast zmniejszony dwukrotnie (rys. 7).

Ponieważ konfiguracja płaska 01x, 01 y, Olz jest obrazem konfiguracji przestrzennej trzech odcinków o wspólnym początku i parami prostopadłych, możemy ją uważać za pewne odwzorowanie naroża sześcianu (o pozostałych krawędziach równoległych odpowiednio do 01x, Oly, Olz).

Obraz przedstawiony na rysunku 7 powstanie przez rzutowanie równoległe sześcianu na płaszczyznę rzutni (rysunku) równoległą do ściany tylnej (x, z) i kącie promieni rzutujących różnym od 90° w stosunku do rzutni. W takim odwzorowaniu przednia i tylna ściana sześcianu (obie równoległe do rzutni) nie uległy

23