1002889897

określając rzut równoległy podajemy miary kątów a i fi. Mając a i fi możemy wyznaczyć kierunek wektora. W zależności od miary kątów a i fi, niektóre rzuty równoległe mają nazwy. np. dla a = arcctg H = 63 stopnie mamy rzutkawaleryjski, dla 45 stopni mamy rzut wojskowy (gabinetowy).

(10 linijek tekstu których nie mam, trzeba je wziąć najlepiej od Epiego)

Rzut perspektywiczny

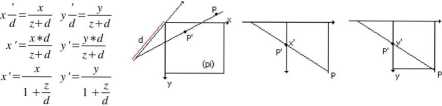
Widzimy, że odległość 'z' decyduje o wielkości wyświetlanego obiektu. Im 'z' wieksze tym wyświetlany obiekt jest mniejszy.

Macierz perspektywy (współrzędne

		1	0	0		0
		0	i	0		0
Ker	=	0	0	0		0
		0	0	1		1
				d
1	0		0	0				X
0			0	0		X		y
0	0		0	0	*	y	=	0
			1			z
0			_	1		1		^+i
			d					d

jednorodne)

Przyjmijmy teraz, że rzutnia (pi) leży w płaszczyźnie XY oraz obserwator znajduje się w punkcie £(*₀’>Wo)⁼Uo>    ~d)    ■

d=-z0    z    d=-z0    z

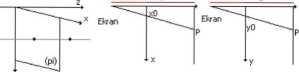
y

Z podobieństwa trójkątów

r x_Q_x-x₀ y y₀_y-y₀

Z~Zq ~Zq Z~Zq

. x-x₀

’l-.Ł

Zo

- Izlo

y=—~+y₀

Zo

i