1102

Tablica 5.7. Zestawienie miar zróżnicowania dla przykładu 5.1

Parametr	Klasa A	Klasa B
Średnia arytmetyczna x	4	4
Odchylenie przeciętne dt	0,5	1.7
Odchylenie standardowe St	0.7	2,12
Współczynnik zmienności \	12,5%	42,5%
Współczynnik zmienności	17,5%	53%

Źródło: obliczenia własne

Z obliczonych współczynników zmienności wynika, że uczniowie klasy B są bardziej zróżnicowani pod względem liczby błędów popełnionych w dyktandzie.

W celu obliczenia niektórych z klasycznych miar dyspersji można również wykorzystać arkusz Excel. Poszczególne miary można wyznaczyć korzystając z następujących funkcji statystycznych:

•    odchylenie przeciętne: Odch.Średnie,

•    odchylenie standardowe: Odch.Standardowe.

Funkcje te dotyczą jednak tylko szeregów szczegółowych. W przypadku obliczania pozostałych miar zróżnicowania, w tym zwłaszcza dla szeregów rozdzielczych, można wykorzystać podstawowe operatory matematyczne i znacznie szybciej niż przy pomocy kalkulatora dokonać obliczeń, które my umieszczamy w pomocniczych tablicach.

5.2. MIARY ASYMETRII (SKOSNOSCI)

Kolejnym etapem analizy struktur)'jest badanie asymetrii, czyli skośności szeregu. W analizie szeregów strukturalnych można się spotkać z przypadkiem, że badanie średniego poziomu cechy oraz dyspersji nie obrazuje dostatecznie istnienia różnic między szeregami, a bardziej szczegółowa obserwacja szeregu wyklucza podobieństwo analizowanych zbiorowości. W takim przypadku posługujemy się miarami asymetrii (skośności). Dzięki tym miarom możemy się zorientować, czy odchylenia od wartości średniej (centralnej) w jedną stronę są mniej lub więcej liczne od odchyleń w drugą stronę. Analizując np. poziom płac w przedsiębiorstwie, ] obliczyliśmy średnią płacę i chcemy ustalić, czy liczba pracowników, których pła- 1 ca jest wyższa od płacy średniej jest większa czy mniejsza od liczby pracow ników, j których płaca jest niższa od płacy średniej.

Okazuje się, że istotny jest nie tylko przeciętny poziom i zróżnicowanie cechy, ] ale także to, czy przeważająca liczba badanych jednostek ma wartość cechy powyżej czy poniżej przeciętnego poziomu. Zagadnienie to można zbadać za pomocą

miar asymetrii, które opieramy na spostrzeżeniu, że w szeregu symetrycznym średnic (x, Mc, D₀) są sobie równe.

Szereg symetryczny to taki szereg, w którym liczebności rozkładają się w sposób identyczny po obu stronach przedziału dominanty. Zachodzi wówczas równość:

x — Me = D₀    (5.11)

Rys. 5.1. Rozkład symetryczny

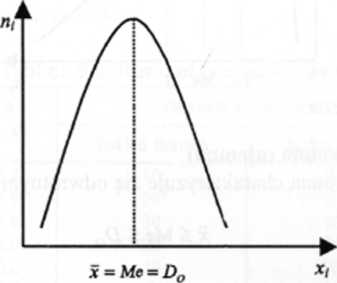
Źródło: opracowanie własne.

Różnica między średnią arytmetyczną a dominantą służy jako miara asymetrii, jest to tzw. wskaźnik asymetrii (A_s), który mierzy nic tylko stopień asymetrii lecz także wskazuje na jej kierunek:

A_s=x-D₀.    (5.12)

W szeregu symetrycznym wskaźnik asymetrii wynosi zero:

x-D₀= 0.

Jeżeli szereg nic posiada własności 5.11, wartości miar średnich odbiegają od siebie, jest szeregiem asymetrycznym. Asymetria może być prawo- lub lewostronna, a wskaźnik asymetrii przyjmuje wartość większą lub mniejszą od zera. W przypadku asymetrii:

•    prawostronnej (dodatniej): x-D₀ >0,

•    lewostronnej (ujemnej): x-D₀< 0.

Asymetria prawostronna (dodatnia)

Jak pokazano na rysunku 5.2. relacja między' średnią arytmetyczną, medianą/' dominantą jest w przypadku asymetrii prawostronnej następująca:

D₀ <, Mc <i x    (5.13)

143