0069

71

§ 5. Całki eliptyczne

Z geometrycznego punktu widzenia wiążemy całkę Abela (1) z tą krzywą algebraiczną, która określona jest równaniem (2). Na przykład całka

(3)

J R (x,]/ax² + bx+c ) dx

związana jest z krzywą drugiego stopnia y² = ax²+bx+c.

Jeśli krzywa (2) może być przedstawiona parametrycznie równaniami

x = rft), y = r₂{t)

tak, że funkcje r_t(t) i r₂(t) są wymierne (w tym wypadku krzywa nazywa się jednobieżna (*)), to w calce (1) można sprowadzić wyrażenie podcałkowe do postaci wymiernej, podstawienie x = r, (f) sprowadza je mianowicie do postaci

J?0t(O, r₂(t))r'ft)dt.

Do klasy tej należą oba wspomniane wyżej przypadki. W szczególności możliwość sprowadzenia do postaci wymiernej wyrażenia podcałkowego w całce typu (3) związana jest z tym właśnie faktem, że krzywa drugiego stopnia jest jednobieżna [281, 282].

Oczywiście zmienne x i t związane są równaniem algebraicznym, a więc t jest funkcją algebraiczną zmiennej x. Jeśli rozszerzyć klasę funkcji elementarnych włączając do niej także wszystkie funkcje algebraiczne, możemy powiedzieć, że w przypadku jednobieżności krzywej (2) całka (1) da się zawsze wyrazić w postaci skończonej przez funkcje elementarne.

Taka sytuacja jest jednak w pewnym sensie wyjątkowa. Na ogół krzywa (1) nie jest jednobieżna, a wówczas, jak można udowodnić, całka (1) na pewno nie zawsze, tzn. nie dla każdej funkcji R, może być wyrażona w postaci skończonej, chociaż możliwość ta nie jest wykluczona dla pewnych konkretnych R.

Napotykamy to już przy rozpatrywaniu ważnej klasy całek

(4) I R (x, j/nx³ + bx² + cx+d ) dx, J R(x, ^ax⁴+bx³+cx²+dx+e dx

zawierających pierwiastek kwadratowy z wielomianów stopnia 3-go i 4-go i zbliżonych do całek (3). Całki typu (4) nie wyrażają się już z reguły w postaci skończonej przez funkcje elementarne nawet przy rozszerzonym rozumieniu tego terminu. Dlatego też zapoznanie się z nimi odłożyliśmy do ostatniego paragrafu, aby nie przerywać zasadniczej linii wykładu w tym rozdziale, poświęconym przede wszystkim zbadaniu tych klas całek, które mogą być obliczone w postaci skończonej.

O wielomianach pod pierwiastkiem we wzorach (4) zakłada się, że mają współczynniki rzeczywiste. Oprócz tego będziemy zakładali zawsze, że nie mają one pierwiastków wielokrotnych, gdyż w przeciwnym razie można by było wynieść spod pierwiastka czynnik liniowy, zadanie sprowadziłoby się wówczas do całkowania wyrażeń zbadanych już wcześniej i całka wyraziłaby się w postaci skończonej. To ostatnie może się niekiedy zdarzyć także, gdy nie ma pierwiastków wielokrotnych. Łatwo jest na przykład sprawdzić, że

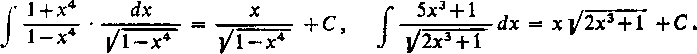
(’) Można dać także czysto geometryczną definicję krzywej jednobieżnej, nie będziemy się jednak na tym zatrzymywali.