9

10 A S lnjiit Ilu, ,V\ w. im flrklmmcchciniczne dla elektryków

• geometrycznymi jeśli relacje te są wyłącznie między współrzędnymi;

• kinematycznymi - jeśli relacje te występują również między pochodnymi współrzędnych względem czasu.

,<7„) = 0 7=1.....m

Dodatkowo więzy kinematyczne dzielimy na holonomiczne (całkowalne), to znaczy takie, które można za pomocą całkowania sprowadzić do więzów geometrycznych. Pozostałe noszą nazwę nieholonomicznych. W zdecydowanej większości układów elektromechanicznych mamy do czynienia z więzami skleronomicznymi, geometrycznymi i kinematycznymi holonomicznymi.

Podstawowym równaniem wykorzystywanym w analizie systemów elektromechanicznych jest równanie d’Alamberta~-Lagrange’a [1] w postaci:

fT d dL dL

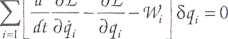
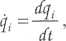
L - funkcja Lagrange’a równa różnicy między całkowitą koenergią kinetyczną układu a jego całkowitą energią potencjalną, hq_i - przesunięcie przygotowane i-tej współrzędnej,

W i - wymuszenia o charakterze niepotencjalnym.

Funkcja Lagrange’a określana jest jako różnica między całkowitą koenergią kinetyczną układu a jego całkowitą energią potencjalną. Wyrażenie na koenergię kinetyczną można określić za pomocą jej związku z energią kinetyczną w następujący sposób:

n

E_K{q_x,...,q„, Pi,---, P_ll) + E_Ka{q_l,...,q_i},q_[,...,q_n)=Y_Jp_iq_i (2.2)

Rozwiązanie równania (2.1) jest możliwe na dwa sposoby:

1)    gdy funkcja Lagrangc’a jest wyrażona za pomocą współrzędnych niezależnych,

2)    z wykorzystaniem mnożników nieoznaczonych Lagrange’a.

W przypadku pierwszym równanie (2.1) jest słuszne dla dowolnej kombinacji przesunięć wirtualnych (przygotowanych), w tym także wtedy, gdy wszystkie tc przesunięcia są równe zeru z wyjątkiem jednej kombinacji, zatem:

d_dL_ dt dq_t

= i = l.

(2.3)

a równanie to nosi wtedy nazwę równania Lagrange’a drugiego rodzaju.

W drugim przypadku wystarczy zauważyć, że więzy tak geometryczne, jak i kinematyczne liniowe można przedstawić w postaci:

n

2^c;^^+c>o=° j =    (2.4)

i=i

gdzie m jest liczbą równań więzów. Zatem wariacje wirtualne współrzędnych układu muszą spełniać związki:

£^=0/ = l.....»    (2.5)

i=l

Jeśli teraz pomnożyć równanie (2.5) przez nieoznaczone na razie mnożniki La-grange’a Xj ^ 0 i dodać je stronami, to otrzymamy:

(2.6)

(2.7)

;=i «=i

Dodając stronami równania (2.1) i (2.6), otrzymujemy:

d dL dL .    . L _A

Teraz mnożniki nieoznaczone można potraktować jako dodatkowe zmienne. Wystarczy zauważyć, że jeśli na n zmiennych narzucone jest m równań więzów, to n tn zmiennych jest od siebie liniowo niezależnych. Można zatem dla m zmiennych zależnych tak dobrać mnożniki nieoznaczone, aby wyrażenie w nawiasie relacji (2,7) zerowało się, natomiast dla zmiennych niezależnych zerować się mu-nimIo < )nIMlecznie więc otrzymujemy układ równań: