starosol12

M = -

(g + qV;

16

(3.96)

gdzie l_n jest rozpiętością w świetle, określoną zgodnie z rys. 3.80.

Gdy rozpiętości sąsiednich przęseł są różne, do obliczenia momentów podporowych przyjmuje się rozpiętość większą.

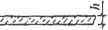
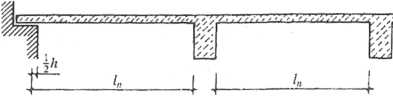
Rys. 3.80. Zasady określania rozpiętości w świetle przy obliczaniu płyt metodą plastycznego wyrównania

momentów

Do wyznaczenia minimalnych momentów w przęsłach wewnętrznych płyty należy, przy przyjęciu momentów podporowych z wzorów (3.94), (3.95), założyć, że na rozważane przęsło działa obciążenie g_p = g + 0,25q (patrz procedura według rys. 3.83b). Zasięg momentu podporowego w przęśle skrajnym (odcinek a na rys. 3.83b) można wyznaczyć bezpośrednio z wzoru

a =

(3.97)

Dla płyt, których rozpiętości różnią się więcej niż o 20% norma [N62] nie podaje sposobu obliczania.

W tym przypadku obliczenia rozpoczyna się od przęsła o największej rozpiętości. Jeżeli przęsłem tym jest przęsło skrajne, to moment na krawędzi powinien być zawarty w granicach

(3.98)

Cg + ⁽l )^ll

14

Jeżeli zaś przęsłem o największej rozpiętości jest przęsło wewnętrzne, to wartość momentu zginającego na krawędzi podpory powinna się mieścić w przedziale

(g + q)il

24

0% + 16

(3.99)

Zaleca się przyjmowanie wartości większych z nierówności (3.98) i (3.99). Po ustaleniu momentu na krawędzi podpory przęsła o największej rozpiętości, określa się kolejno momenty przęsłowe i podporowe w pozostałych przęsłach z podstawowego warunku

M₀-

M^L + M^P    (g + q )l„

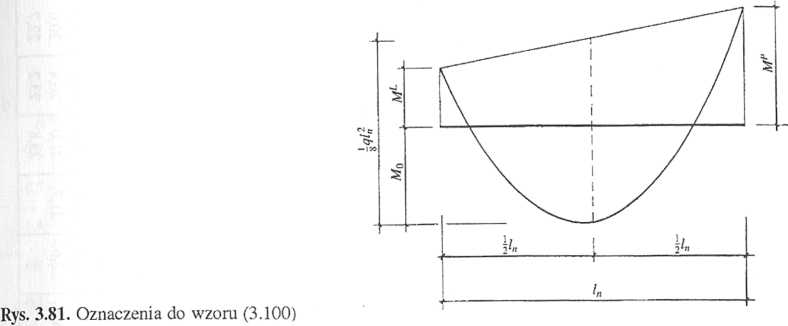
(3.100)

dla którego oznaczenia podano na rys. 3.81.

Dla ułatwienia obliczeń podano w tabl. 3.8 [201] współczynniki m, pozwalające obliczyć moment przęsłowy przy znajomości momentów podporowych. Za pomocą tej tablicy można także obliczyć moment podporowy przy przyjęciu momentu przęsłowego i pozostałego momentu podporowego. Wyrażenie m = <» oznacza podporę przegubową (skrajną).

Przykład. Dany jest element jak na rys. 3.82, dla którego g = 2,0 kN/m, q = 1.5 kN/m. Przy wykorzystaniu tablic sporządzono obwiednie momentów, przedstawione na rys. 3.82b przyjmując, że I_A__B = /.

Dla obliczeń z uwzględnieniem plastycznego wyrównania momentów obciążenie g + q = 3,5 kN/m. Długość w świetle przęsła A-B

l_n = /-—= 0,958/, 24

przęsła B-C

l_n = 1,3/ - — = 1,217/. " 12

Momenty podporowe w przęśle większym B-C: przyjęto

M_b = M_c

_ (g+ <?)/« _ 3,5(1,217/)² __or/|/2 16 16

Ponieważ m^L = m^P = 16, zatem zgodnie z tabl. 3.8 m = 16, więc

M_B__c = ^-⁺ -— = 0 324/².

16

Moment przęsłowy w przęśle A-B: moment podporowy M_n = 0,324/" można wyrazić, uwzględniając różnice rozpiętości, jako

M

u

(g + g)l²n _ 3,5(0.958/)"

0.324/²,

skąd