starosol7

Rysunek 3.71 h jest konsekwentnym przeniesieniem pomierzonego wykresu pracy przekroju (rys. 3.65i) na element ciągły. Jeżeli pominiemy wpływ: sił poprzecznych, stopniowego włączania się do pracy pojedynczych wkładek itp., będzie to wykres dość dobrze odpowiadający sytuacji rzeczywistej, oczywiście przy traktowaniu elementu zarysowanego jako pewnego kontinuum materialnego.

Jeżeli dany jest rozkład sztywności wzdłuż długości elementu, można dla każdego określonego obciążenia q_t obliczyć rozkład momentów. Określenie rozkładu momentów zginających wzdłuż długości belki przy znajomości rozkładu sztywności pozwala na jednoznaczne określenie jej ugięć.

W miarę zwiększania intensywności obciążenia statycznie niewyznaczalnego elementu żelbetowego otrzymujemy kolejne przebiegi momentów zginających. Jeżeli w dowolnym przekroju tego elementu wartości momentów nie są przy narastających obciążeniach proporcjonalne do tych obciążeń, oznacza to, że następuje przegrupowanie sił, czyli redystrybucja momentów. Jeżeli proporcje te są utrzymane, redystrybucja nie zachodzi.

Prześledzimy zagadnienie na przykładzie belki zamocowanej na dwóch końcach (rys. 3.72) [198]. W belce takiej traktowanej jako sprężysta

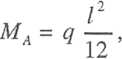
^Mi=~^q—_Ą^{; st}3^d

M,

= 2.

Pierwsze zarysowania (pod obciążeniem q_cr) powstaną w przekroju podporowym takiej belki, w konsekwencji zmniejszy się sztywność stref podporowych i nastąpi zwiększanie przyrostów momentów przęsłowych. Gdy zarysowuje się przekrój przęsłowy, następuje częściowe wyrównanie sztywności przekrojów przęsłowych i podporowych, a momenty podporowe będą silniej wzrastać niż przęsłowe.

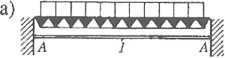
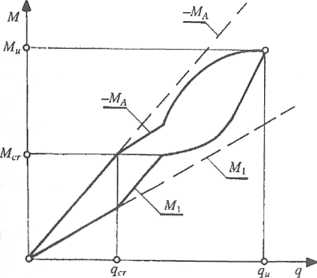
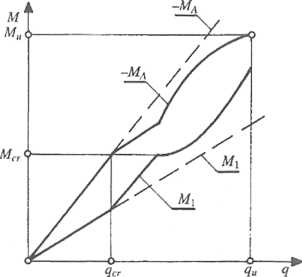
Rys. 3.72. Redystrybucja zupełna i częściowa w belce obustronnie utwierdzonej: a) schemat obciążenia, b) redystrybucja zupełna, c) redystrybucja częściowa.-----przebieg momentów według teorii sprężystości

Jeżeli przekroje mają odpowiednią zdolność odkształceń plastycznych, to gdy momenty podporowe osiągną wartość zbliżoną do nośności M_u, nastąpi w tej strefie bardzo silny spadek sztywności. W konsekwencji zaczną szybko wzrastać momenty przęsłowe tak, że w końcu nośność przekroju podporowego i przęsłowego zostanie osiągnięta wspólnie, pod tym samym obciążeniem q_u. W belce nastąpi pełna redystrybucja. Ilustracją takiego zachowania się belki jest rys. 3.72b.

Jeżeli zaś zdolność odkształcenia (np. przekroju podporowego A) jest w obszarze bliskim zniszczenia M_u ograniczona, to może dojść do zniszczenia tego przekroju, zanim zostanie osiągnięta nośność przekroju przęsłowego 1. Jest to tzw. redystrybucja częściowa, przedstawiona na rys. 3.72c.

O przebiegu redystrybucji momentów w elemencie decydują czynniki materiałowe i konstrukcyjne.

Do czynników materiałowych należy zaliczyć:

•    cechy betonu (odkształcalność w zależności od obciążenia, odkształcalność graniczną, odkształcalność Teologiczną),

•    cechy stali (jej ukształtowanie — gładka, żebrowana, odkształcalność, występowanie lub brak wyraźnej granicy plastyczności).

Do czynników konstrukcyjnych należą:

•    wymiary i sposób podparcia elementów,

•    sposób zazbrojenia (liczba i rozmieszczenie prętów zbrojeniowych, strzemionowanie),

•    sposób obciążenia (rozmieszczenie obciążeń i charakterystyka ich narastania). Czynniki te były analizowane przez wielu autorów — tutaj zwrócimy uwagę na niektóre z nich.

Wpływ wytrzymałości betonu na redystrybucję momentów nie jest duży, jeżeli znajdujemy się w strefie normalnie stosowanych betonów konstrukcyjnych. Ogólnie można powiedzieć, że redystrybucja jest większa dla betonów o mniejszej wytrzymałości.

Jest rzeczą oczywistą, że najkorzystniejsza z uwagi na redystrybucje momentów jest stal gładka mająca wyraźną granicę plastyczności. Jednakże badania, m.in. Ryżyńskie-go i Wołowickiego oraz Glenszczyk [51], potwierdziły pełną przydatność w tym względzie także stali żebrowej bez wyraźnej granicy plastyczności.

Następnym podstawowym zagadnieniem jest pytanie, czy zagwarantowanie wystarczającej odkształcalności poszczególnych przekrojów jest wystarczające do uzyskania całkowitej redystrybucji momentów. Otóż okazuje się, że jest to niewystarczające dla tych elementów ciągłych, w których może nastąpić zniszczenie jednego przęsła, pod-

.....

+-^-1---+-£-+■

l\ > /o > ń

Rys. 3.73. Przykład lokalnego wyczerpania nośności