Str 107

Q =

sina

h₂

j b\[z<\z.

"i

Współczynnik wydatku p wprowadzony do wzoru ma sens identyczny jak przypadku otworów małych i można orientacyjnie przyjmować jego wartość za 0,6. Należy zwrócić uwagę, że b jest funkcją zagłębienia z i funkcja ta

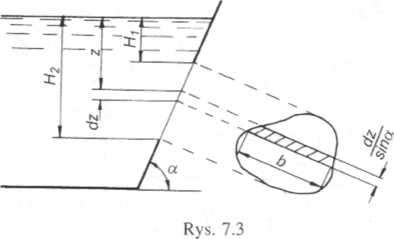
musi być określona na podstawie warunków geometrycznych otworu przed wykonaniem całkowania. Wyprowadzony wzór nie uwzględnia prędkości dopływowej i ewentualnej różnicy ciśnień w zbiorniku i na zewnątrz. W przypadku konieczności uwzględnienia któregoś z tych elementów należy umownie

podnieść zwierciadło wody o wysokość równoważną różnicy ciśnień ———,

au₀    Y

.ub o wysokość prędkości -. Spowoduje to wzrost z o tę wartość.

2g

Wypływ z otworu zatopionego

Rozpatrujemy schemat pokazany na rys. 7.4. Napiszmy równanie Ber-noulliego dla dwóch przekrojów poziomych odpowiadających poziomom wody w obu zbiornikach. Stosując oznaczenia jak na rysunku otrzymamy

Po "0 p V¹ ,

Zn ⁺ — + — = z + — + — + > h._r.

* Y 2g    Y 2g ^ *'^r

Rozpatrując wyraz h_s[r widzimy, że mamy w tym przypadku do czynienia z dwiema stratami lokalnymi, gdyż straty na opory ruchu w samym zbiorniku są bardzo małe wobec znikomej prędkości dopływu wody.

= C — (gdzie - pręd-4g

Pozostają więc: strata na wlocie do otworu h

kość w otworze) i strata przy nagłym rozszerzeniu przekroju (tabl. 4. ID)

107