str019

R o 7. d z i a 1 2

OBLICZANIE 1'RZEWYŻSZEŃ I WYSOKOŚCI; POMIARY MIMOŚRODOWE; WYZNACZANIE WARTOŚCI j WSPÓŁCZYNNIKA REFRAKCJI

V    i

2.1. OBLICZENIE PRZEWYŻSZENIA Z OBSERWACJI JEDNOSTRONNYCH NA PODSTAWIE a^ob, D, PRZY ZNANEJ WARTOŚCI k WSPÓŁCZYNNIKA REFRAKCJI

Przewyższeniem Ah nazywamy wysokość celu E nad powierzchnią horyzontu, Wysokość tę liczy się wzdłuż pionu punktu E. Na rys. 2.1 przewyższenie przedstawia; odcinek AE.

Zakładając, że znamy długość D łuku 1A na poziomie instrumentu, kąt a"^H| obarczony błędem refrakcji oraz wartość k współczynnika refrakcji, wyprowadzimy; wzory na przewyższenie Ah.

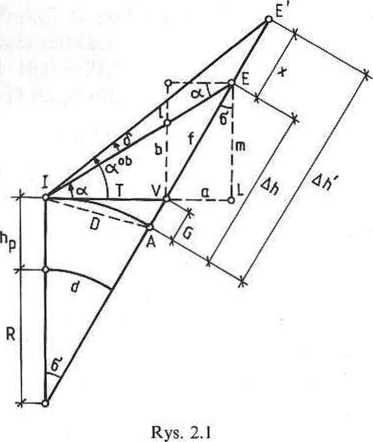
Postawione zadanie można rozwiązać dwoma sposobami. Pierwszy z nich polega na wyeliminowaniu kąta refrakcji <5 z zaobserwowanego kąta pionowego ot^ob (rys. 2.1) i wykorzystaniu w rachunku zależności geometrycznych, wiążących kąt cc pozbawiony wpływu refrakcji z wielkościami D oraz R. W drugim sposobie obliczenie przewyższenia przeprowadza się wykorzystując kąt a°\ obarczony błędem refrakcji. Wpływ kąta Ó eliminuje się odejmując od obliczonej wartości przewyższenia liniowy składnik refrakcji x. Podamy rozwiązanie obu omówionych przypadków.

) /

i I mil IC/.ENIHPR/EWY ź\/l NI \ M \ PODSTAWI!’) KĄTA PIONOWEGO /.WYELIMINOWANYM KĄTEM REIRAKCJI

i .......ii/ zakładamy, że długość l) luku oraz współczynnik refrakcji k są znane,

ni', obliczyć ki{t refrakcji a na podstawie (1.65)

V _ P • k. D 2R cosa*’^1'	(2.1)
■ |i|" s/y cosa^0h « 1, dla k = 0,13, R =6382 otrzymamy
5" = 2,10 D ł.	(2.2)
Iff 5^tc = 6,48 • D	(2.3)
I.. |ii/ pozwala obliczyć kąt a ze związku
oc = a^ob — S	(2,4)
koizyslać go do obliczenia przewyższenia. iHidiiie z rysunkiem 2.1 mamy
Ah = G + f	(2,5)

. i k.bokość horyzontu G jest prostą funkcją długości łuku D, (utożsami.me| iii I l-il'I z illugością odpowiadającej mu cięciwy), więc zadanie sprowadza się do ..i ii • ma długości odcinka VE - f, którą, z uwagi na małą wartość kąta ć>. można ii ni 11 ć z długością odcinka LE = m. Przyjmiemy więc

f = m    (2.6)

u «* b dy

Ah = m + G

Mamy jednak

m = b + 1    (2.7)

liny i zyin

b = T ■ tg a    (2.8)

1 = a - tga    (2.9)

i po dokonaniu podstawienia otrzymamy

Ah = T • tg a + G + a • tg cc    (2.10)

lok widać, zadanie polega teraz na obliczeniu długości odcinka a. Ponieważ •linuno odcinek, jak i kąt a są małe, więc przyjmiemy

f % b

u ląd

a = f • sin <r    b ■ sin a = T ■ tga • sin a = T • Iga ■ —

(2.11)