Zdjęcie1203

mm

Błąd len można wyeliminować z wyniku pomiaru poprzez wprowadzenie poprawki, tj. wartości którą należy'dodać algebraicznie do l/.w ..surowego” wyniku w celu uzyskania wyniku poprawnego. Błąd systematyczny. którego prawdziwą wartość nie jest znana, ocenia się za pomocą gttmiey #_v takiej. Ze wartość jego leży zawsze w przedziale 16s₍. czyli

ł?„ “ ± fiSi

Przy wielu zmiennych wpływających graniczny błąd systematyczny szacuje się w sposób probabilistyczny:

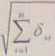
tiif

Mimo, ze nie należ)' go interpretować jako zmiennej losowej, gdyż dla każdego zdarzenia tna on zawsze tą samą. co prawda nieznaną wartość.

Ocena błędów przypadkowych, które zawsze moją charakter losowy, opiera się na modelu probabilistycznym.

2, PRAWDOPODOBIEŃSTWA ZDARZENIE LOSOWEGO

Równanie obserwacje będący zmienną losową, tzn. pod wpływem różnorodnych czynników przypadkowych przyjmujący różne wartości, wcześniej nie wiadomo jakie, może być nieciągły (dyskretny) albo ciągły.

Przykładami zmiennych losowych są: wymiary przedmiotów obrabianych, niezawodność, afagifwri narzędzi skrawających, własności materiałów itp.

Do oceny liczbowej zajścia zdarzenia; przypadkowego A stosuje się tzw. „prawdopodobieństwo”. mówiące, ile jest możliwych zdarzeń danego m do ogólnej liczby zdarzeń n

P(A)= -

n

W tym celu należy przeprowadzić badania. Jednak przeprowadzenie pełnych badań dla całej populacji generalnej polegających na wszechstronnym badaniu własności zjawiska lub obiektu w badaniach technicznych ■lubinnych jest praktycznie niewykonalne wmoiłiwymd© przyjęcia czasie. % tego względu na równi z definicją klasyczną prawdopodobieństwa stosuje się definicję statystyczną:

n

adzje: - n - liczba doświadczeń, w których pojuwiln się zdarzenie A n - ogólna Iiczba doświadczeń Fą - liczebność względna (częstość względna)

3, WARTOM OCZEKIWANA I ŚREDNIA ARYTMETYCZNA

Warta# tKzektwiftw zrmennef losowej ciąglćj określona jest wzorem:

* |y/(.V)t/A‘

f( * gęstość prawdopwdohijńsj W M