Image16 (30)

121 Rozw iązania zadań ze zbioru "MENDLA "

1 m³ • 300 kPa

3^r~

PB = 100 kPa

/.Is

Vc

Z równania gazu doskonałego dla stanów B i C otrzymamy: PB • Vb pc • Vc Tb ” Tc

PC =

stąd pc =

PB • Vb • Tę Tb • Vc

Z wykresu odczytamy:

Pb = 100 kPa , Vb = 3 m³

T_c = 150 K" , T_B = 100K, V_c = 4/rr³

100 kPa -3 m³-150 K 100 K ■ 4 m³ pc = 112,5 kPa

Ze stanu C do D gaz przechodzi izochorycznie (V = const.), więc rysujemy prostą przechodzącą przez początek układu i punkt C. Zaznaczamy odcinek CD.

Ze stanu A do D można gaz przeprowadzić izobarycznie, więc:

Pa = po-

Odp.: Przemiany z wykresu V(T) pokazano w układzie p(T) na wykresie nr II.

Zadanie 627 str.126

Jeżeli gaz jest sprężany od objętości Vi do V2 w naczyniu nieprzewodzącym ciepła, to mamy przemianę adiabatyczną.

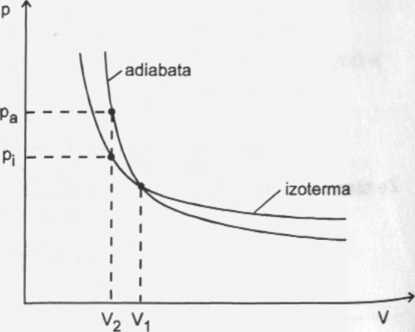
Na podanym wykresie możemy porównać ciśnienia gazu po sprężeniu od objętości Vi do V2 dla obu przemian.

Przy sprężaniu izotermi-cznym gazu przyrost ciśnienia jest mniejszy niż przy spężaniu adiabatycznym. Dla V2 mamy pa > Pi.

Przy sprężaniu izotermi-cznym pi Vi = p2 V2 za zwiększenie ciśnienia jest odpowiedzialne zmniejszenie się objętości. Natomiast w wyniku sprężania

adiabatycznego zmniejsza się objętość i jednocześnie rośnie temperatura, a więc przy-^st ciśnienia w tej przemianie jest większy, co wypływa bezpośrednio z równania stanu gazu:

n . \/

p-V

= n

p =

n-R-T

Zadanie 628 str.126

Dane:

_tl„10°c stąd Ti = 273 /(+10 /< = 283 K _pi = 100 kPa

V, = 10 dm³

V₂ = Sdm³ V₃ = V1 = 10 d/rr³

Szukane:

t₃ = ?

V(T) = ? P(V) = ?

Ti =T2 - przemiana izotermiczna P3 = p2 - przemiana izobaryczna

W stanie początkowym gaz ma parametry:

pi = 100/cPa, Vi = 10 dm³ oraz Ti=283 K W wyniku przemiany izotermicznej gaz osiągnął stan 2 o parametrach: T2 = Ti = 282 K oraz V2 = 5 dm³ Dla tej przemiany zachodzi związek:

Pi • Vi = p2 • V2 /: V2

pi • Vi

P2 =

P2 =

V₂

100 /cPa

10 drrP

5 dm³ P2 = 200 kPa

Ze stanu 2 do trzeciego gaz przeprowadzono izobarycznie, więc jego parametry mają wartość:

p₃ = p2 = 200 kPa oraz Dla przemiany izobarycznej mamy:

V₂ V₃

V₃ = 10 dm³

Ta T₃

T₃ • V₂ = T₂

t₂-v₃

T₃ =

T3 =

V₃ /: V₂

v₂

283 K ■ 10 dm³

5 dm³ T₃ = 566 K