47352 Image44 (17)

175 Rozw iązania zadań ze zbioru "MENDLA

Pierwsza i druga zasada termodynamiki Zadanie 681    str.135

Dane:

Szukane:

Q

30 kJ- (najprawdopodobniej 30 kJ    AT = ?

a nie 50 kJ, jak podano w zbiorze).

Pi

P2

V1 V₂

300 kPa = 300000 Pa 100 kPa = 100000 Pa 0,1 m³ 0,25 rri³

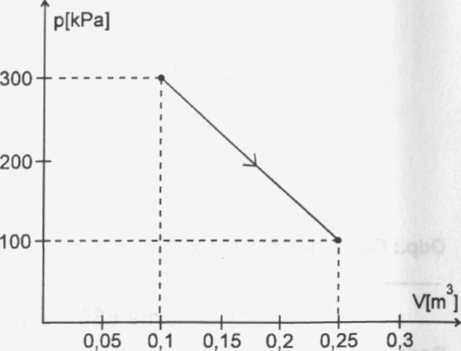
Zgodnie z I zasadą termodynamiki AU = W + Q, gdzie W = - p • AV

Ciśnienie zmienia się liniowo, więc weźmiemy pod uwagę ciśnienie średnie: Pśr = ^fil|-^,aAV = V2-V,

Po podstawieniu do pracy W mamy:

_{w =} _£L|P2._(V2_V₁)

W = - ^OOOOPa+IOOOOOPa _(Q^__Q^_}

W = - 200000Pa • 0,15/rr³ ,    Pa = -^

nr

W = - 30000-^ • m³ ,    N-m=J

nr

w = - 30 kJ

Gaz wykonał pracę 30kJ, więc możemy obliczyć jego energię wewnętrzną. AU = - 30kJ + 30kJ = 0

__Rozwiązania zadań ze zbioru "MENDLA"_176

Energia wewnętrzna AU gazu nie zmieniła się , więc jego temperatura również nie ulega zmianie, czyli AT = 0

Odp.: Temperatura gazu nie uległa zmianie.

Dane:

k = 1,66

p = 28-²- = 0,028-^-.

mol    mol

R = 8,31

Zadanie 682 str.135

Szukane:

c_p = ? - ciepło właściwe przy stałym ciśnieniu c_v = ? - ciepło właściwe przy stałej objętości

K • mol

9i

Cv

K =

A C_v , gdzie

C_p - ciepło molowe przy stałym ciśnieniu C_v - ciepło molowe przy stałej objętości

Cp — Cv • K

Z definicji ciepła molowego otrzymamy:

c„__Qe_

^Cp n • AT

Podstawimy do C_p = k • C_v

Q_d    Q_v

stąd

= K

/•n

C_v =

Qv

n • AT

n • AT n • AT Teraz obie strony równania podzielimy przez m.

gdzie n - ilość moli gazu

up Q_v AT ^{= K} ' AT

Q

/: m

gdzie

m - masa gazu

Otrzymaliśmy związek:

Qp    Q_v

= K

m • AT m-AT’

lecz z definicji ciepła właściwego wiadomo, że

Cv =

Qv

c_p =

Qc

m • AT

Więc po podstawieniu mamy:

Cp — K • Cv

Z równania Mayera otrzymamy:

Cp ⁼ R + C_v

Za C_p i C_v podstawimy odpowiednie wzory,

m-AT*

stąd

Q

Qv

/• n

n • AT n • AT Teraz obustronnie dzielimy przez masę m gazu.

'2 — Zeszył 5