Image5 (59)

14    _Rozwiązania zadań ze zbioru "MENDLA"

Jednostki

[ V ] = Pa n? =-^r ■ m³ = J nr

U = |- 10 000 = 15 000 = 15 kJ Odp.: Energia wewnętrzna jest równa 15kJ.

Zadanie 542 str.108

Dane:

V= 1,38/rr⁵ k = 1,38-10~²³

Szukane:

N = ? - liczba cząsteczek

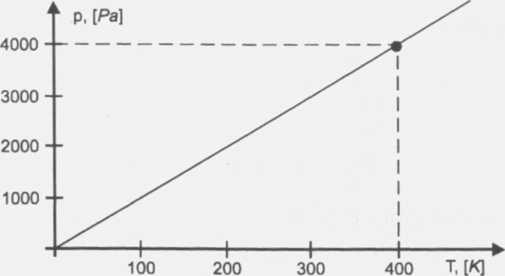
Z wykresu odczytujemy, że dla temperatury T = 300K ciśnienie gazu wynosi p = 3000 Pa.

Korzystamy z równania stanu gazu doskonałego.

Py- = N-k /: k

N = ^ k-T’

N

Pamiętamy, że Pa = —^

oraz

J= Nm

Jednostki

N 1 =

JH „3 Pa-m³ m²

1 _K

k^k

N•m_ J J ~J~

_N_ 3000-1,38    __1Q24

1,38-10^-23-300

Odp.: Liczba cząsteczek wynosi 10²⁴.

Dane:

= 0,028-^2. mol

T = 282K

R = 8,31

J

mol• K

Zadanie 543    str.108

Szukane:

Uśr = ?

Wychodzimy ze związku średniej energii kinetycznej cząsteczek gazu z jego temperaturą.

3

Ekśr = 2 • k-T, ale średnią energię kinetyczną wyraża się również wzorem:

m

• lir

Ekśr =

gdzie m - masa cząsteczki

|kT = ^ _A2

m • i|r = 3k T /: m 3-k-T

Dśr =

m

Po obustronnym pierwiastkowaniu

ośr

^v m

Masa cząsteczki m jest równa stosunkowi masy molowej p do liczby cząsteczek Na zawartej w jednym molu.

—*

Po podstawieniu otrzymamy:

Na

lecz k-NA = R, -/3RT

stąd vśr = V „ Jednostki:

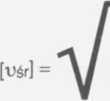
mol ■ K _ *1 J ■ mol kg ~ V mol ■ kg mol