Image51 (15)

189 Rozwiązania zadań ze zbioru "MENDLA"____

W₃ = n.R.^.T₂-nR -

T₂    t₂

T₃ Ti

W₃ = n • R • T₃ - n • R •    ¹

T2

W ostatniej przemianie ochłodzono gaz zachowując stałą objętość, więc praca W₄ = 0.

Ostatecznie praca W całego cyklu będzie:

W = Wi + W₂ + W₃ + W₄

W = - n • R • (T₂ - Ti) + 0 + n • R • T₃ - n ■ R •    + 0

• 2

W = n • R • (T1 - T₂ + T₃ -    )

12

W=1 mol• 8,31 ^ ^J ■.. (300K- SOOK + 800K-

K■ mol    600K

W = 8,31p- 100/C

A

W = 831 J

Odp.: W tym cyklu nad gazem wykonano pracę 831 J.

Zadanie 691 str.138

Dane:    Szukane:

S, m, Ti, p, M, Q, po, c_v    Ft = ? - siła tarcia

m — masa azotu M — masa odważnika

Fi, F₂ — siły parcia azotu na tłok Q — ciężar odważnika F — siła parcia atmosferycznego na tłok

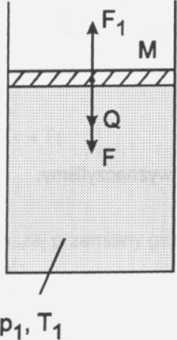
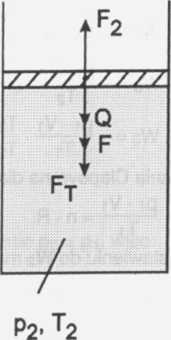
Z równowagi sił w II przypadku otrzymamy: F₂ = Q + F + F_t /: S

ś

f₂ q f fi

S " s ⁺ s ⁺ s

Z definicji ciśnienia wiadomo, że p = ^ , więc:

Fi    F₂    F

^p1 ” S ’    ^P2~ S ' ^Po_S

Po podstawieniu pi, p2 i po do wcześniejszego równania wyznaczymy siłę tarcia Ft. Q _ Ft

^P2 = s ^{+ P}°⁺ s

/•s

P2 • S = Q + po • S + Ft Ft = P2-S-_Po-S-Q Ft = S • (p2 - po) - Q

W równaniu nie znamy wartości p2, ale możemy je wyznaczyć. Ponieważ azot pobrał ciepło Q zachowując stałą objętość, więc:

Q = Cv ■ m • ńT i fŁ-B _>    _ Pi_j2

Ti T2    Ti

oraz AT = T2 - Ti Po podstawieniu:

Q = c_v • m • (T2-T1)    /: c_v • m

Przekształcając to równanie obliczymy T2.

Q

c_v • m

T₂ =

= T₂-Ti

Q

c_v • m

+ Ti

Wyznaczoną T2 podstawiamy do równania p2 =

Pi T2

P1 • (

Q

skąd p2 =

c_v • m

+ Ti)

Pi

Ti

Q + c_v • m • Ti

P2 =

Cv • m

P2 =

Pi -(Q + c_v • m • Ti)

c_v • m • Ti

Wreszcie P2 możemy podstawić do siły tarcia Ft

*pi -(Q + Cvm-Ti)

c_v • m • Ti ^f Q *

F_T = S • stąd Ft = S •

-Po

Pi

+ 1

-Po

- Q , -M -g

ale Q = Mg

m • c_v • T1

Odp.: Siłę tarcia Ft tłoka o ścianki cylindra przedstawia ostatnia zależność.