img297 (7)

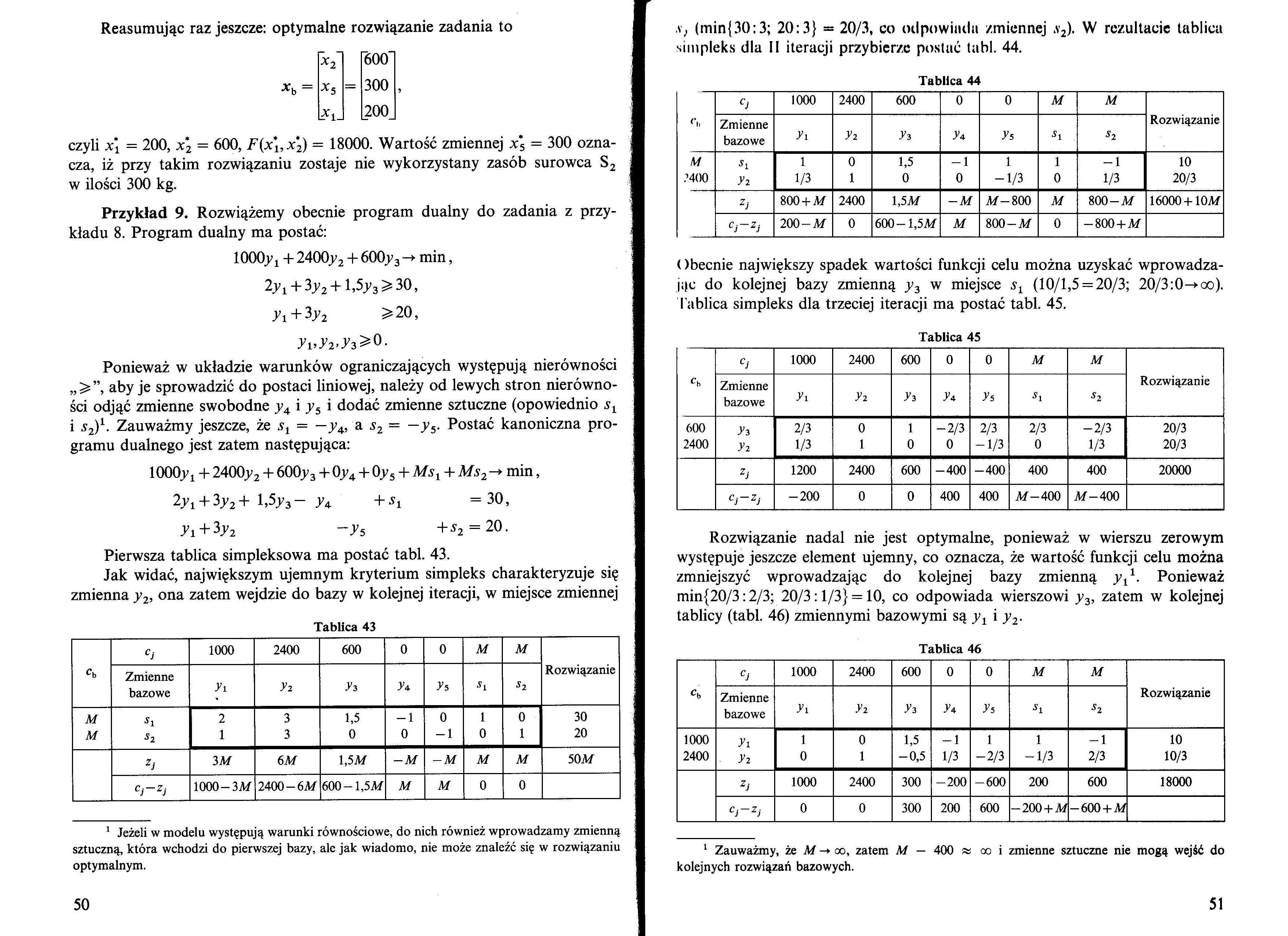
Reasumując raz jeszcze: optymalne rozwiązanie zadania to

	*2~		600'
*b =	*5	=	300
	*1_		200.

czyli x\ = 200, x₂ = 600, F(x\,x\) = 18000. Wartość zmiennej x*₅ = 300 oznacza, iż przy takim rozwiązaniu zostaje nie wykorzystany zasób surowca S₂ w ilości 300 kg.

Przykład 9. Rozwiążemy obecnie program dualny do zadania z przykładu 8. Program dualny ma postać:

lOOOy ₃ + 2400>'₂ + 600y₃ -> min,

2ji + 3y₂ + l,5y₃ ^ 30, y_t + 3y₂    5*20,

Ponieważ w układzie warunków ograniczających występują nierówności „ ^ ”, aby je sprowadzić do postaci liniowej, należy od lewych stron nierówności odjąć zmienne swobodne y₄ i y₅ i dodać zmienne sztuczne (opowiednio s_l i s₂y. Zauważmy jeszcze, że s_t = —y₄, a s₂ = —y₅. Postać kanoniczna programu dualnego jest zatem następująca:

lOOOy₃ + 2400>'₂ + 600y₃ + 0y₄4-0y₅ + Ms_t + Ms₂~* min,

2ji + 3y₂ + l,5y₃—    +s_t    =30,

y₁ + 7>y₂    -y_s    +5₂ = 20.

Pierwsza tablica simpleksowa ma postać tabl. 43.

Jak widać, największym ujemnym kryterium simpleks charakteryzuje się zmienna y₂, ona zatem wejdzie do bazy w kolejnej iteracji, w miejsce zmiennej

Tablica 43

cb	^CJ	1000	2400	600	0	0	M	M	Rozwiązanie
	Zmienne bazowe	Ji	y2	Ja	Ja	Ja		*2
M		2	3	1,5	-1	0	1	0	30
M	s2	1	3	0	0	-1	0	1	20
	^z)	3 M	6 M	1,5M	— M	— M	M	M	50 M
	^ci~^zi	1000 - 3M	2400-6M	600-1.5M	M	M	0	0

¹ Jeżeli w modelu występują warunki równościowe, do nich również wprowadzamy zmienną sztuczną, która wchodzi do pierwszej bazy, ale jak wiadomo, nie może znaleźć się w rozwiązaniu optymalnym.

■V; (min{30:3; 20:3} = 20/3, co odpowiada zmiennej ,v₂). W rezultacie tablica simpleks dla II iteracji przybierze postać tabl. 44.

Tablica 44

	^CJ	1000	2400	600	0	0	M	M	Rozwiązanie
	Zmienne bazowe	y i	y2	y3	V4	y 5		ij
M		i	0	1,5	-1	i	1	-1	10
.7400	y 2	1/3	1	0	0	-1/3	0	1/3	20/3
		800 + M	2400	1,5 M	— M	s: i oo 8	M	OO O 0 1 *	16000+10M
	^ci~^zi	200-M	0	600—ł,5Af	M	800 -M	0	-800 + M

< )becnie największy spadek wartości funkcji celu można uzyskać wprowadzając do kolejnej bazy zmienną y₃ w miejsce (10/1,5 = 20/3; 20/3:0->-oo). Tablica simpleks dla trzeciej iteracji ma postać tabl. 45.

Tablica 45

	^ci	1000	2400	600	0	0	M	M
	Zmienne bazowe	Zi	y2	y3	y4	y 3	•Sl	*2	Rozwiązanie
600	y 3	2/3	0	1	-2/3	2/3	2/3	-2/3	20/3
2400	y2	1/3	1	0	0	-1/3	0	1/3	20/3
	^ZJ	1200	2400	600	-400	-400	400	400	20000
	^c!~^zi	-200	0	0	400	400	S i 8	M—400

Rozwiązanie nadal nie jest optymalne, ponieważ w wierszu zerowym występuje jeszcze element ujemny, co oznacza, że wartość funkcji celu można zmniejszyć wprowadzając do kolejnej bazy zmienną y₁¹. Ponieważ min{20/3:2/3; 20/3:1/3} = 10, co odpowiada wierszowi y₃, zatem w kolejnej tablicy (tabl. 46) zmiennymi bazowymi są y_± i y₂.

Tablica 46

cb	^CJ	1000	2400	600	0	0	M	M	Rozwiązanie
	Zmienne bazowe	y i	y2	y 3	y4	y3	•Sl	s2
1000	y i	i	0	1,5	-i	i	1	-1	10
2400	. y2	0	i	-0,5	1/3	-2/3	-1/3	2/3	10/3
	^zj	1000	2400	300	-200	-600	200	600	18000
	^ci~^zi	0	0	300	200	600	— 200 + M	— 600 + M

51

1

Zauważmy, że M -» oo, zatem M — 400 « oo i zmienne sztuczne nie mogą wejść do kolejnych rozwiązań bazowych.