skanuj0092 (28)

C. Grupy przestrzenne trójwymiarowe

L Opis

Grup tych jest 230. Opisują one 230 różnych sposobów prawidłowego rozmieszczenia w przestrzeni elementów symetrii w przypadku nieskończonych zbiorów okresowych trójwymiarowych.

Również w tym przypadku grupa przestrzenna jest wynikiem połączenia typu sieci z grupą punktową należącą do tego samego układu. Osiami tej grupy są osie zwykłe lub osie śrubowe. Płaszczyzny symetrii są zwykłymi płaszczyznami symetrii lub płaszczyznami poślizgu.

Nie jest tu możliwe systematyczne zestawienie zespołów elementów symetrii tych wszystkich grup przestrzennych.

Tych 230 grup przestrzennych jest opisanych w „International Tables for X-Ray Crystallography”, 1.1, ICynoch Press, Birmingham.

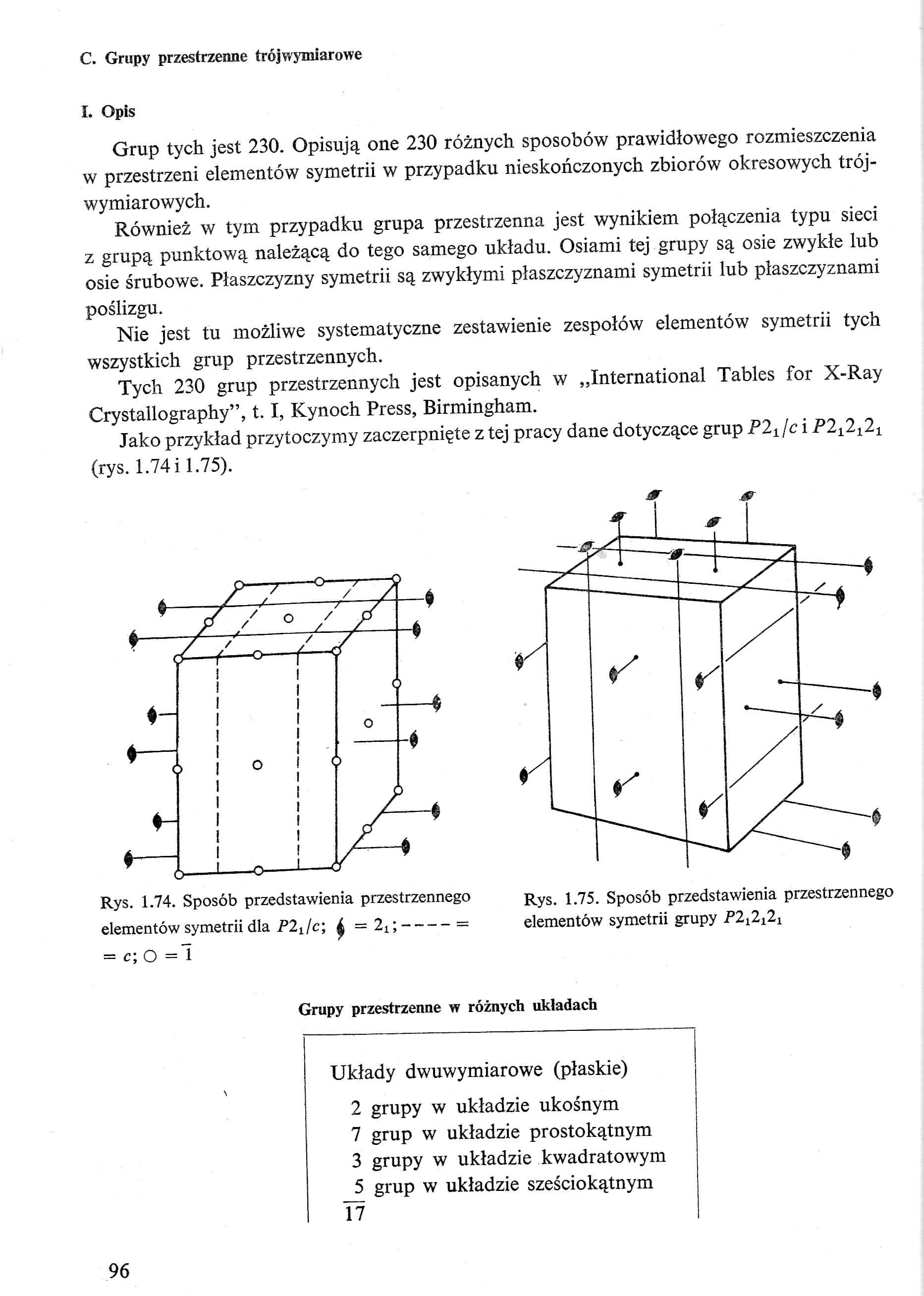
Jako przykład przytoczymy zaczerpnięte z tej pracy dane dotyczące grup P2_±/c i P2₁2₁2₁ (rys. 1.74 i 1.75).

Rys. 1.74. Sposób przedstawienia przestrzennego

elementów symetrii dla P2_tlc; Ą = 2₁;-----

= c; 0=1

Rys. 1.75. Sposób przedstawienia przestrzennego elementów symetrii grupy P2_l2₁2₁

Grupy przestrzenne w różnych układach

Układy dwuwymiarowe (płaskie)

2    grupy w układzie ukośnym

7 grup w układzie prostokątnym

3    grupy w układzie kwadratowym 5 grup w układzie sześciokątnym

Ti

96