skanuj0078 (29)

1.2.4.2, Grupy przestrzenne a układy krystalograficzne

Sieć i grupa punktowa w sensie rozszerzonym, zdefiniowanym poprzednio, powinny być z sobą zgodne, w innym bowiem przypadku nastąpiłaby częściowa utrata symetrii jednej lub drugiej.

a)

<0

17 7)    17 7

IZ 71    tz 71

v ^

k zł

©

V 71    [7 7]

h. A    [Z    A

n    ©    $

1771	77	l/\|
M	M b . ... - 4	17 Z]
77	77'	77
M i	M $	& ^

m    m

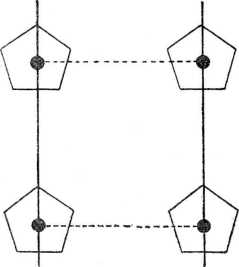
Rys. 1.63. Symetria motywu powinna być zgodna z symetrią sieci.

a)    Motyw o symetrii kwadratowej (4mm) połączony z siecią prostokątną (typ p) tworzy tylko zespół o symetrii prostokątnej (pmm), gdyż osie czterokrotne motywu nie są operatorami symetrii sieci, a w związku z tym całego zbioru.

b)    Również motyw o symetrii prostokątnej (2mm) połączony z siecią kwadratową tworzy tylko zbiór nieskończony o symetrii prostokątnej (pmm). W tym przypadku osie czterokrotne sieci nie mogą być operatorami symetrii motywu.

c)    Motyw pięciokątny foremny (grupa 5m)

powtarzany przez sieć kwadratową (4mm). Jedynym wspólnym elementem motywu i sieci jest płaszczyzna zwierciadlana m:    grupa

płaska pm w przypadku pokrywania się płaszczyzn motywu i sieci. W innym przypadku byłyby grupa p\!

82