str063 (5)

5 9. SZEREG LAURENTA I PUNKTY OSOBLIWE 63

ozwijają się w zbieżne szeregi

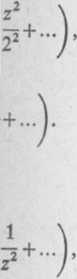
w pierścieniu 0<|z— 11 <2. !) rozkładamy najpierw naszą

Mamy wówczas

(3)

Z założenia zmienna z przebiega pierścień

0<|z —1|<2.

Iz- II

Wynika stąd natychmiast, że

<1. Wobec tego funkcję/₂(z) określoną wzorem (2)

rozwijamy na szereg geometryczny zbieżny

1    1    11 lT z-1 (z-1)²    1

(4)    “zTl ^_z-l + 2 ~T"    7-i~ TL¹ 2~⁺

1+-—-

Podstawiając wzór (4) do wzoru (3), mamy kolejno

00

dla 0 < |z 11 < 2.

m

B = 0

Stąd

a„ =

(_!)«+» ^1 v ' 2^n+2	dla	n> 0,
i	dla	n = -1,
0	dla	n<-1.

Zadanie 9.4. Jakiego rodzaju punkty osobliwe odosobnione różne od nieskończoności mają funkcje

a) /(z) =

1

z² + l’

±    sin z

b) /(z) = e * , c) /(z) ---?

Rozwiązanie, a) Funkcja nasza ma w punktach z = i oraz z = — i bieguny jednokrotne, ponieważ funkcja l//(z) = z² + l ma w tych punktach zera jednokrotne.

b) funkcja /(z) = e^l,z ma w punkcie z=0 punkt istotnie osobliwy, bo już przy zmiennej

rzeczywistej z= .v nie istnieje granica lime^1/*. Mamy bowiem

*-0

_i_    j_

lim e^x = 0 oraz lim e^x = co .

*-o-o    *—o+o