Image012 (58)

Jerzy Chramiec, Stanisław Lindner

praszającym. Ponieważ w wyniku rozpraszania całkowita energia sygnału informacyjnego nie zmienia się, zatem w wyniku X-krotnego poszerzenia szerokości pasma następuje /(-krotne zmniejszenie widmowej gęstości mocy sygnału użytecznego. Zasada rozpraszania bezpośredniego jest zilustrowana na rys. 1.16.

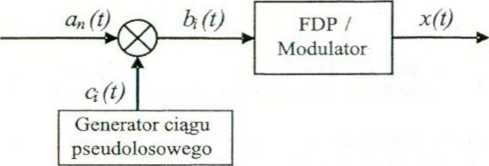
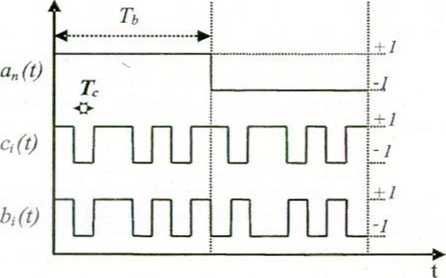
Rys. 1.16. Schemat nadajnika i zasada rozpraszania bezpośredniego w dziedzinie czasu,

FDP - filtr dolnoprzepustowy.

W omawianym procesie rozpraszania bardzo istotne jest właściwe dobranie ciągów rozpraszających. Wymaga się, aby funkcje korelacji skrośnej poszczególnych par ciągów rozpraszających miały wartości zerowe, a funkcja autokorelacji przyjmowała także wartość zerową dla niezerowego przesunięcia czasowego. Parametry statystyczne ciągu rozpraszającego powinny być jak najbardziej zbliżone do parametrów szumu białego. Stąd też wywodzi się ich określenie - ciągi pseudolosowe.

Dzięki takim właściwościom ciągów rozpraszających jest możliwe wykorzystanie tego samego pasma przez wielu użytkowników stosujących różne ciągi pseudolosowe. Oznacza to, że w tym samym paśmie, miejscu i czasie zasoby systemu mogą być współużytkowane przez wielu użytkowników.

W odbiorniku sygnał o postaci /(?)= x(t)+«(/) odebrany z zaszumionego kanału

jest poddawany demodulacji, w wyniku czego otrzymuje się ciąg odtworzony {r/t))=\b.(t)\ © («///[. Wydzielenie sekwencji danych polega na wymnożeniu sekwencji odtworzonej przez zsynchronizowany względem ciągu rozpraszającego, taki sam ciąg rozpraszający {c/t)) jaki został wykorzystany w nadajniku.

W wyniku przeprowadzenia operacji skupiania widma otrzymuje się

sjt) = [{b/t)\y{n/t)}]{c/t)}= ajt)[c/t))\c/t))+ [n/t)}[c/t)} (1.9)

Ponieważ symbole ciągu rozpraszającego c.(t) przyjmują wartości bipolarne ±1, iloczyn elementów ciągów [c/t))[c/t)) jest zawsze równy jeden. Sygnał sjt) jest więc sumą składowej wolnozmiennej ajt) i szybkozmiennej której wartość funkcji ko

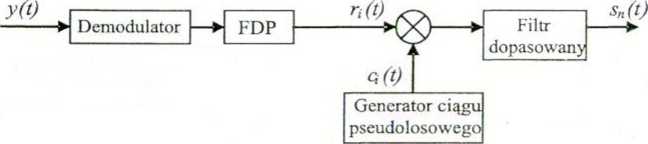
relacji jest bliska zero ze względu na brak korelacji szumu z sekwencja rozpraszającą. W rezultacie zostaje skupiona moc sygnału .danych, a sekwencja sjt) jest odtworzoną sekwencją informacyjną ajt) Operacja ta nosi nazwę operacji skupiania widma i została przedstawiona na rysunku 1.17.

i	7c o
n(t)	"iruui	LTUITL	±i -i
g(0	irurr	innr	jj +1
Sn(t)	n <■■■■■-...........-......-»		-i -►

Rys. 1.17. Schemat odbiornika i zasada skupiania widma w dziedzinie czasu.

Proces rozpraszania i skupiania widma w dziedzinie częstotliwości został zilustrowany na rysunku 1.18.