Image43 (16)

84

Zate

• I

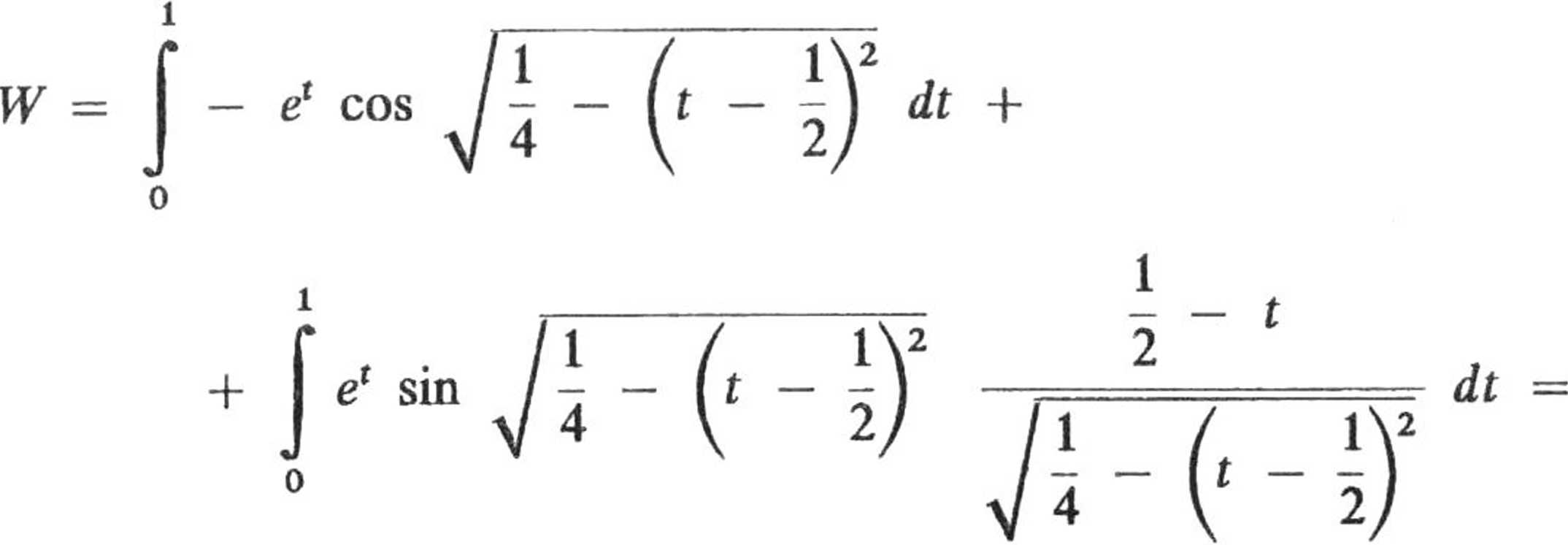
e — 1.

Sprawdza

sposób.

warunki Schwartza: rot F = = er* siny,

SJj

dx

e^x siny.

Pole sił jest więc polem potencjalnym, praca elementarna -zupełną

dW =F_xdx + F_ydy= —e* cosy dx -f e^x siny dy,

tak że można całkować po dowolnej drodze, np. po prostej y = 0 w zmienności x : [1, 0]. Otrzymamy

różniczką

przedziale

o

W — —\e^x cosO dx = — e^x

o

= e — 1

2.23. Drogi całkowania przedstawiono na rys.27.

a.

W₁ = F dr =

F_x dx

-1

x² dx

1

— V

3

2

3’

-1

gdyż y = 0, z = 0.

b. W celu obliczenia całki krzywoliniowej po drodze l₂ przejdziemy do współrzędnych biegunowych (r, (p):

COS(p,

y

sm(p,

gdyż Ir =1. Stąd

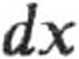
— sinę d(p.

Zatei

w,-i	F dr = 1 (x^2 -f y^2) dx =	0 — I sin(p d(p = cos(p
J ^l2	J ^l2	J — JL

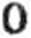
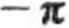
2.24. Pole siły F(r) nazywamy potencjalnym (i zachowawczym), jeżeli istnieje jednoznaczna funkcja skalarna E_p(r\ taka że

F = -grad E_p.

Pokażemy, że dla takiego pola zachodzi warunek

0.

rot F

Załóżmy, że rot F ^ 0 i istnieje taka funkcja ę?, że F = —grad cp. Stąd

rot grad cp — — rot F ^ 0,

co jest sprzeczne z tożsa

II

ością

rot grad (p = 0,

prawdziwą dla każdej funkcji skalarnej <p, klasy C².

Zatem słuszne jest twierdzenie, że energia potencjalna E_p (r) jest określona tylko w przypadku bezwirowego pola sił F(r), tzn.

rot F = 0.