Image43

84

Zate

II

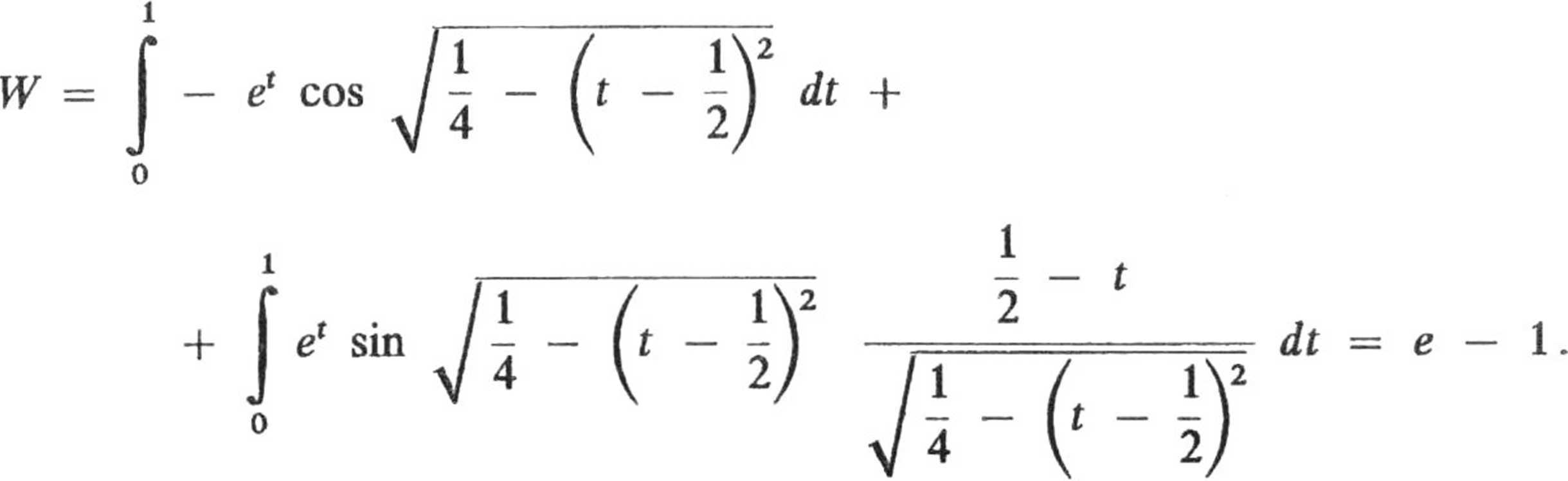
II sposób. Sprawdzamy warunki Schwartza: rot F = 0

e* siny,

⁸h

dx

e* siny.

Pole sił jest więc polem potencjalnym, praca elementarna - różniczką zupełną

dW

b_x dx + t_y dy

tak że można całkować po dowolnej drodze, np. po prostej y = 0 w przedziale zmienności x ; [1, 0]. Otrzymamy

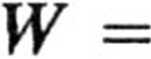
0

J e^x cosO dx =

1

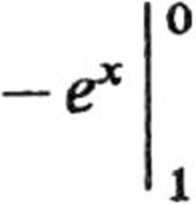
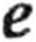
2.23. Drogi całkowania przedstawiono na rys.27. a.

_Wl = | F dr = | F _x dx =

“I

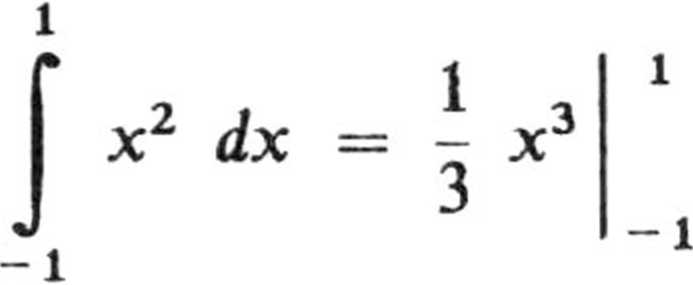
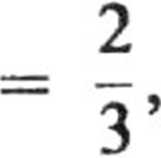
gdyż y = 0, z = 0.

b. W celu obliczenia całki krzywoliniowej po drodze l₂ przejdziemy do współrzędnych biegunowych (r, cp):

Rys.27

x — cos (p,

y

smcp,

gdyż Ir = 1. Stąd

dx — — sinę dcp.

Zate

o

o

W, = I F dr

(x² -|- y²) dx =

sin(p dcp

cos cp

= 2

i

i

— TL

— K

2.24. Pole siły F(r) nazywamy potencjalnym (i zachowawczym), jeżeli istnieje jednoznaczna funkcja skalarna E_p (r), taka że

F = -grad E_p.

Pokażemy, że dla takiego pola zachodzi warunek

0.

rot F

Załóżmy, że rot F ^ 0 i istnieje taka funkcja cp> że F = —grad cp. Stąd

rot grad cp = — rot F # 0,

co jest sprzeczne z tożsamością

rot grad cp = 0,

prawdziwą dla każdej funkcji skalarnej cp, klasy C².

Zatem słuszne jest twierdzenie, że energia potencjalna E_p (r) jest określona tylko w przypadku bezwirowego pola sił F(r), tzn.

rot F = 0.