img228 (3)

9. Sygnały losowe 2.doc, 11/18

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

prawdziwa jest ogólna zależność pomiędzy momentami sygnału losowego X(t):

o\{t)= E[x\t)} -

zatem dla zmiennej losowej m^

^am_XT - ^[^mxT ] “ E \^rnxA

można wykazać, źe warunkiem koniecznym i dostatecznym zerowania się wariancji średniej czasowej

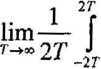
1-

2 T

^o.v(^TV^x = ⁰

9. Sygnały losowe 2.doc, 12/18

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

w sytuacji, gdy znana jest funkcja autokorelacji (autokowariancji), warunek ten stanowi podstawę do weryfikacji właściwości ergodyczności wartości średniej sygnału

można dowieść, że powyższy warunek jest równoważny warunkowi

1 ^T lim—

T}_T°'^vV

do jego spełnienia wystarczy aby

limiJ_OA.(x)=0

T—>00