img229 (2)

9. Sygnały losowe 2.doc, 13/18

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

• ergodyczność funkcji autokorelacji

sygnał jest ergodyczny względem funkcji autokorelacji, jeżeli funkcja ta uzyskana drogą uśredniania w zbiorze realizacji sygnału z prawdopodobieństwem równym 1, jest równa funkcji autokorelacji uzyskanej drogą uśredniania względem czasu jednej realizacji określonej w dostatecznie długim czasie

sygnał losowy jest ergodyczny względem funkcji autokorelacji, jeśli wariancja funkcji autokorelacji uzyskanej drogą uśredniania względem czasu jednej realizacji dąży do zera, gdy przedział czasowy, w którym jest określona realizacja, dąży do nieskończoności

rozstrzygnięcie czy sygnał losowy X(t) jest ergodyczny ze względu na funkcję autokorelacji wymaga znajomości jego momentu czwartego rzędu; zagadnienie to jest znacznie trudniejsze niż badanie ergodyczności wartości średniej

można udowodnić, że dla sygnałów o rozkładzie normalnym wystarczający warunek ergodyczności funkcji autokorelacji ma postać następującą

lim^₀x(^T)= 0

« ergodyczność wariancji

każdy sygnał ergodyczny ze względu na funkcję autokorelacji jest również ergodycznym ze względu na wariancję; sygnał ergodyczny ze względu na wartość średnią sygnału nie musi być ergodyczny ze względu na funkcję autokorelacji; jedynie dla sygnałów o rozkładzie normalnym wystarczające warunki ergodyczności wartości średniej i funkcji autokorelacji pokrywają się

9- Sygnały losowe 2.doc, 14/18

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

• parametry sygnału ergodycznego

stacjonarny sygnał losowy spełniający wystarczające warunki ergodyczności będziemy nazywać sygnałem ergodycznym (sygnał losowy spełniający warunki wystarczające jest ergodyczny ale nie każdy sygnał ergodyczny musi spełniać warunki wystarczające) parametry sygnału ergodycznego określone są następującymi zależnościami

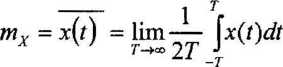
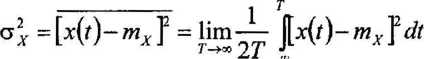
—T

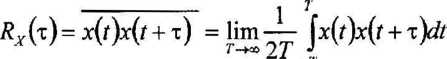
-1