img227 (3)

9. Sygnały losowe 2.doc, 9/18

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

ergodyczność wartości średniej kryterium weryfikacji:

wyznaczenie wartości średniej poprzez uśrednianie względem czasu pojedynczej realizacji procesu w skończonym przedziale czasu a następnie wyznaczenie warunku, przy którym wariancja tak określonej średniej czasowej dąży do zera, gdy czas obserwacji T dąży do nieskończoności (wartość średnia jest wielkością nielosową)

Założenia:

-    sygnał X{t) jest sygnałem stacjonarnym o skończonej wartości średniej m_x

-    x(t) jest realizacją tego sygnału obserwowaną w przedziale czasowym (- T,T) wartość średnia realizacji jest określona wzorem

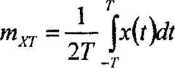
9. Sygnały losowe 2.doc, 10/18

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

jeżeli powyższa całka istnieje dla prawie każdej realizacji sygnału, to tym samym jest określona całka stochastyczna

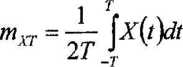
każda realizacja sygnału losowego X{t) może posiadać inną wartość średniej czasowej, zatem m^ będące zbiorem tych wartości jest zmienną losową i nie może być wartością średnią sygnału stacjonarnego

wartość oczekiwana tej zmiennej losowej jest równa wartości średniej sygnału losowego, gdyż zachodzi następujący związek

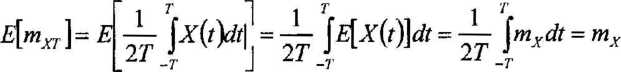
szukamy warunku, przy którym wartość średnia uzyskana w zbiorze realizacji sygnału jest granicą średniej czasowej m_n gdy czas obserwacji T dąży do nieskończoności,

w tym celu badamy wariancję średniej czasowej m_XT (warunek jej zerowania)