img224 (3)

9. Sygnały losowe 2.doc, 3/18

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

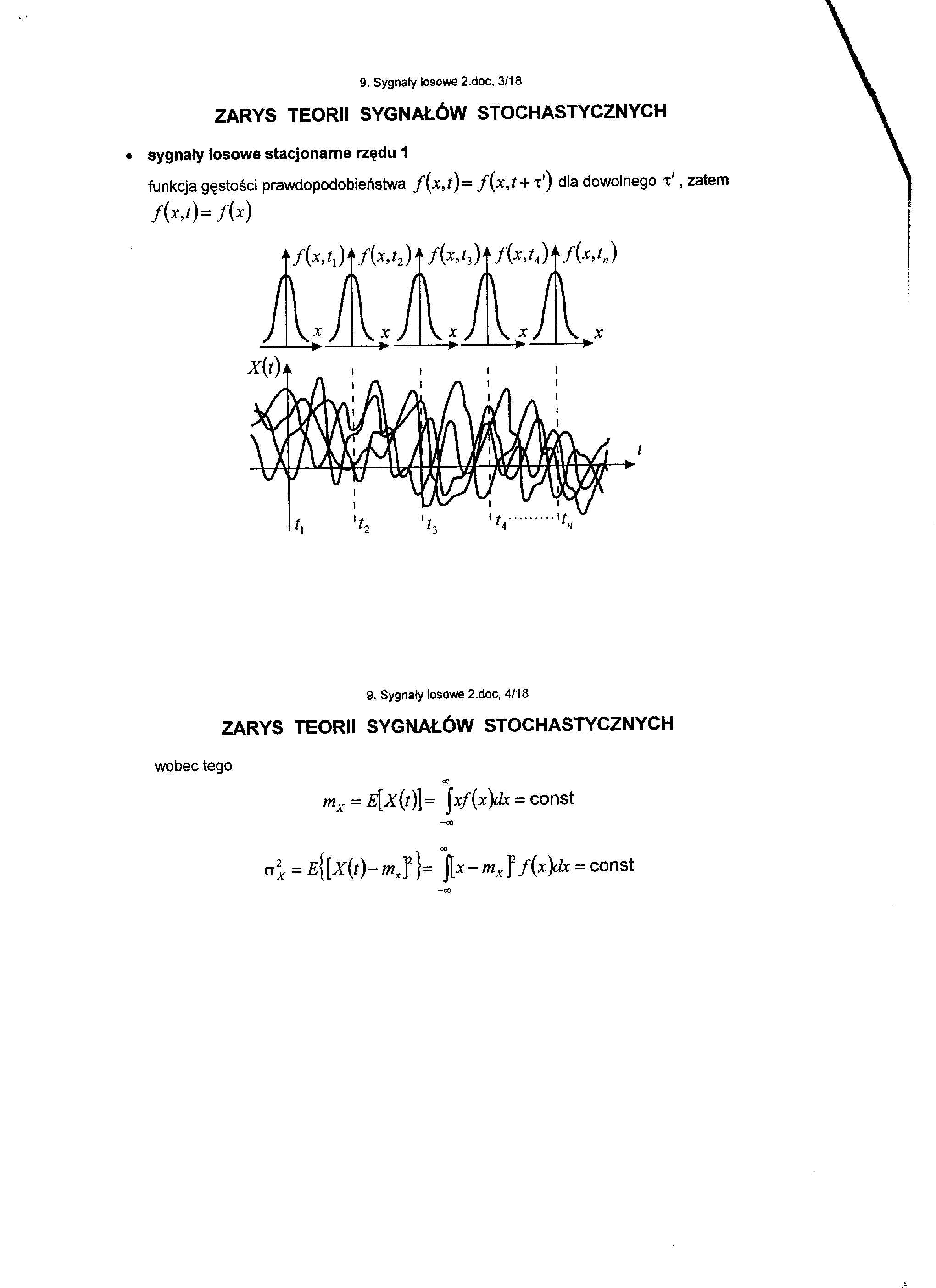
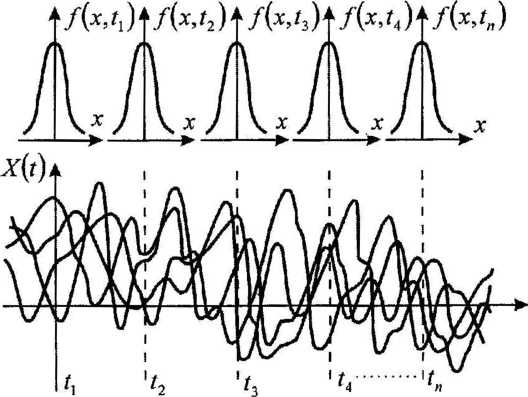
• sygnały losowe stacjonarne rzędu 1

funkcja gęstości prawdopodobieństwa /(*,/)= f(x,t + x') dla dowolnego x', zatem

f(x,t)=f(x)

9. Sygnały losowe 2.doc, 4/18

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

wobec tego

00

m_x - is(Ar(f)] = jxf(x)dx - const v²x = Ą^m;Y }= §.^x~^mxY /(*)* = ^const

—00