80119 img230 (2)

9. Sygnały losowe 2.doc, 15/18

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH Właściwości funkcji autokorelacji sygnałów stacjonarnych

•    funkcja autokorelacji jest symetryczna względem x (f. parzysta)

rA- t)= 4*(r-x)*(/)]=Ąx{t)x{t+T)}=    x)

•    granica funkcji autokorelacji przy t dążącym do nieskończoności, dąży do kwadratu wartości średniej

\imR_x(z)- \imR{x(t)x(t + x)]= m\

T—KO    T-KC

przy x -> oo wartości sygnału mierzone w odległych od siebie momentach są statystycznie niezależne; średni iloczyn niezależnych zmiennych losowych jest równy iloczynowi wartości średnich; wartość średnia sygnału losowego stacjonarnego nie zależy od czasu

♦

lim= limlĄx(t)X(t + x)]= \im{R{x(t)]E[x(t + x)]} = m_xm_x - m_x

t-KO    t—>oo

9. Sygnały losowe 2.doc, 16/18

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

• dla zerowego argumentu funkcja autokorelacji sygnału ergodycznego osiąga wartość maksymalną i jest równa średniej całkowitej mocy sygnału

-T

-T

• wartość średnia sygnału ergodycznego jest równa składowej stałej tego sygnału {kwadrat wartości średniej - moc składowej stałej)

m_x

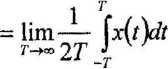
•    wariancja sygnału stacjonarnego jest równa różnicy funkcji autokorelacji dla x = O i x —> oo (różnicą mocy średniej całkowitej i mocy składowej stałej)

<4 =    }= ^(0)- M⁰⁰)

*    funkcja autokowariancji sygnału stacjonarnego jest równa różnicy funkcji autokorelacji i kwadratu wartości średniej

V(*)=    ^RAh-ml