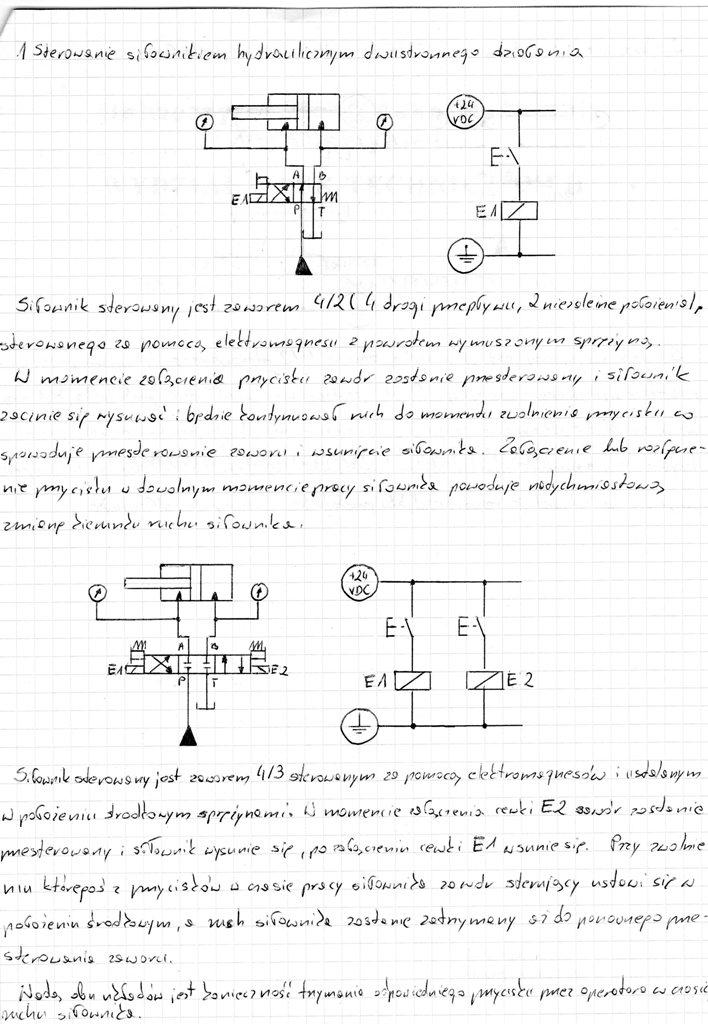
img237 (2)

10. Sygnały losowe 3.doc, 11/29

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

dwuwymiarowa funkcja gęstości prawdopodobieństwa

jednowymiarowy rozkład prawdopodobieństwa normalnego sygnału stacjonarnego zależy tylko od wartości średniej i wariancji a dwuwymiarowy ponadto od funkcji autokorelacji sygnału (można udowodnić, że zachodzi to również dla rozkładu dowolnego rzędu)

dwa sygnały normalne mogą się różnić tylko wartością średnią i funkcją autokorelacji

jeżeli z przesłanek fizycznych wiadomo, żć sygnał jest normalny, to jest on statystycznie wyznaczony jeśli znana jest jego wartość średnia i funkcja autokorelacji

jeżeli sygnał losowy o rozkładzie normalnym jest stacjonarny w szerokim sensie, to jest on również stacjonarny rzędu drugiego

10. Sygnały losowe 3.doc, 12/29

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

jeśli sygnał normalny jest słabo stacjonarny to jest on również ściśle stacjonarny jeżeli wartości sygnału stacjonarnego w przekrojach t i t +1 są nieskorelowane

(r(x)= 0), to są również niezależne

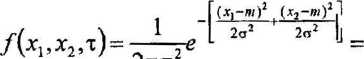
(*1~M)²    ,    Ol-**)²

2c²    1    ~    2<y²

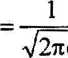
\n a    V27ia

=    t)= /(*, )f(x₂)

liniowa kombinacja sygnałów normalnych również ma rozkład normalny (liniowe przekształcenie sygnału normalnego nie zmienia jego rozkładu)