img245 (3)

1

i

10. Sygnały losowe 3.doc, 27/29

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

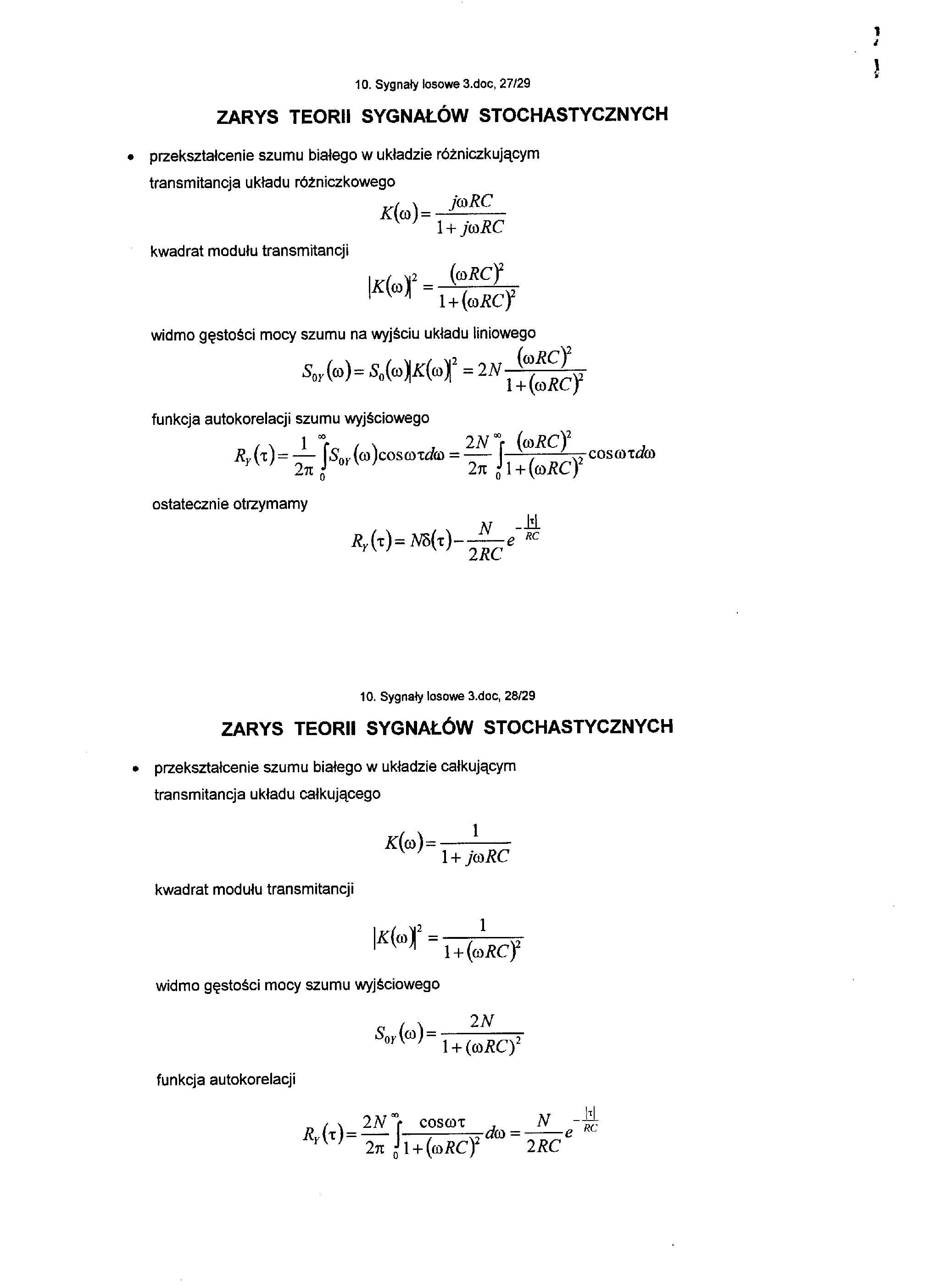
przekształcenie szumu białego w układzie różniczkującym transmitancja układu różniczkowego

K(m) =

j(oRC

1 + jwRC

kwadrat modułu transmitancji

W^!=-Ą ^{1 V} Ą 1

widmo gęstości mocy szumu na wyjściu układu liniowego Ąr(®)= S₀(<o}K{mf =

funkcja autokorelacji szumu wyjściowego

*•^w=Ł )$»«*■»«*»

ostatecznie otrzymamy

^(t)= JV5(t)-

N

> RC

2RC

10. Sygnały losowe 3.doc, 28/29

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

przekształcenie szumu białego w układzie całkującym transmitancja układu całkującego

K(co)=-^l--

^v    ’ 1+

kwadrat modułu transmitancji widmo gęstości mocy szumu wyjściowego

2 N

i + (coi?cy

funkcja autokorelacji

Ji

RC

_n / \    2N°°r coscot , N

R_v(t)=- -7-rra03=-

^V ’    2n    *l + (aRCY2