img243 (3)

10. Sygnały losowe 3.doc, 23/29
ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH
przyjmując
t' = T + Tj — t2 s dxx-dx
otrzymamy
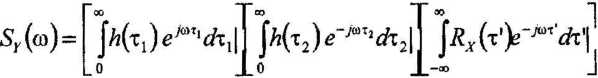
ponieważ
\h{x2y^dx, =
0 “W
ao
^h(x^)ejmidxl - K*(co)
o
4
10. Sygnały losowe 3.doc, 24/29
ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH
zatem
Sr(a )= Ąw)r((o),Sx(® |AT((»))2Sa.(co)
funkcję autokorelacji sygnału po przekształceniu liniowym można zatem wyznaczyć również z prostego wyrażenia
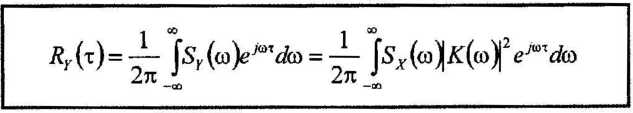
Wyszukiwarka
Podobne podstrony:
img240 (2) 10. Sygnały losowe 3.doc, 17/29ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCHZADANIE znając charak
img237 (2) 10. Sygnały losowe 3.doc, 11/29ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH dwuwymiarowa funkcja
img241 (2) 10. Sygnały losowe 3.doc, 19/29ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH • ZADANIE 2 wyznaczy
img242 (3) 10. Sygnały losowe 3.doc, 21/29ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH ponieważ //(t1)=0 dl
img244 (3) 10. Sygnały losowe 3.doc, 25/29ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH Przejście szumu biał
img245 (3) 1 i 10. Sygnały losowe 3.doc, 27/29ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH przekształcenie
49789 img239 (2) 10. Sygnały losowe 3.doc, 15/29ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH Przejście sygn
więcej podobnych podstron