img244 (3)

10. Sygnały losowe 3.doc, 25/29

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

Przejście szumu białego przez układ liniowy

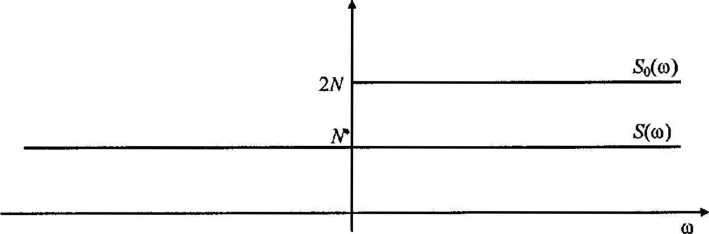
• funkcja gęstości widmowej mocy szumu białego , _x f2,S(co)=2Af dla co>0

sA(o) = •{

[    0 dla co < 0

ff(co) =    _ N dla coe (-00,00)

2

10. Sygnały losowe 3.doc, 26/29

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

funkcja autokorelacji szumu białego

1 °0    tl r OD

R(t) = — [S(ca]e^da = — [e^Kndv = iVS(t)

27t.^JK    2

każda wartość szumu białego jest skorelowana tylko sama z sobą