img320 (3)

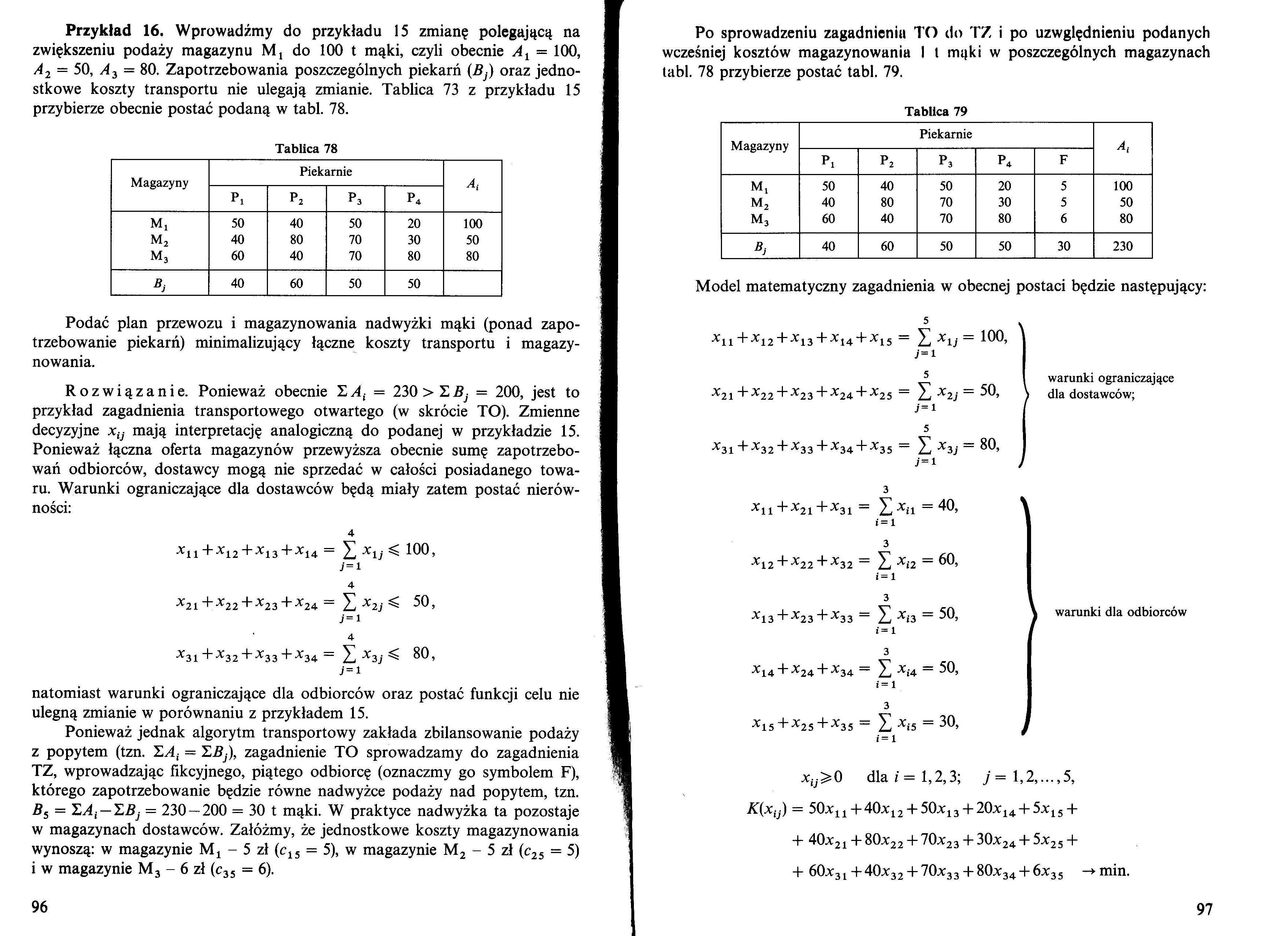
Przykład 16. Wprowadźmy do przykładu 15 zmianę polegającą na zwiększeniu podaży magazynu M, do 100 t mąki, czyli obecnie A₁ = 100, A ₂ = 50, A₃ = 80. Zapotrzebowania poszczególnych piekarń (Bj) oraz jednostkowe koszty transportu nie ulegają zmianie. Tablica 73 z przykładu 15 przybierze obecnie postać podaną w tabl. 78.

Tablica 78

Magazyny	Piekarnie				A,
	Pi	P2	P3	P*
M,	50	40	50	20	100
m2	40	80	70	30	50
m3	60	40	70	80	80
^BJ	40	60	50	50

Podać plan przewozu i magazynowania nadwyżki mąki (ponad zapotrzebowanie piekarń) minimalizujący łączne koszty transportu i magazynowania.

Rozwiązanie. Ponieważ obecnie T,A_t = 230 > ZB, = 200, jest to przykład zagadnienia transportowego otwartego (w skrócie TO). Zmienne decyzyjne x_tj mają interpretację analogiczną do podanej w przykładzie 15. Ponieważ łączna oferta magazynów przewyższa obecnie sumę zapotrzebowań odbiorców, dostawcy mogą nie sprzedać w całości posiadanego towaru. Warunki ograniczające dla dostawców będą miały zatem postać nierówności:

4

*11 +*12 + *13 +*14 = Z *1 j ¹⁰⁰>

1=1

4

*21 + *22 T ^23 + *24 ⁼ Z *2j ^    50 ,

1=1

4

*31+*₃₂+*33+*34 = Z *380,

1=1

natomiast warunki ograniczające dla odbiorców oraz postać funkcji celu nie ulegną zmianie w porównaniu z przykładem 15.

Ponieważ jednak algorytm transportowy zakłada zbilansowanie podaży z popytem (tzn. ZT; = SĄ), zagadnienie TO sprowadzamy do zagadnienia TZ, wprowadzając fikcyjnego, piątego odbiorcę (oznaczmy go symbolem F), którego zapotrzebowanie będzie równe nadwyżce podaży nad popytem, tzn. B_s = 'LA_i — 'LB_j = 230 — 200 = 30 t mąki. W praktyce nadwyżka ta pozostaje w magazynach dostawców. Załóżmy, że jednostkowe koszty magazynowania wynoszą: w magazynie Mj - 5 zł (c₁₅ = 5), w magazynie M₂ - 5 zł (c₂₅ = 5) i w magazynie M₃ - 6 zł (c₃₅ = 6).

Po sprowadzeniu zagadnienia TO do TZ i po uzwględnieniu podanych wcześniej kosztów magazynowania I t mąki w poszczególnych magazynach tabl. 78 przybierze postać tabl. 79.

Tablica 79

Magazyny	Piekarnie
	Pt	Pa	P3	P4	F
M,	50	40	50	20	5	100
m2	40	80	70	30	5	50
m3	60	40	70	80	6	80
Bj	40	60	50	50	30	230

Model matematyczny zagadnienia w obecnej postaci będzie następujący:

⁵ \

X₁₁+Xi2 + Xi3 + X₁4 + X₁₅ = ^ X_xj = 100,

J= 1

5    warunki ograniczające

%21    ^22    *^23    *^24    *25 ~ X ^x2j ~    ) dla dostawców;

j= i

5

^X31 +^X32 + ^X33+^X34 + ^X35 ⁼ X ^X3j ⁼ 80,

3=1

H+%21+^31^- X^Xil— 40,    \

i=l

^C12 + ^X22+^X32    ^Xi2 ^*0,

i = 1 3

^X13 + ^x23    ^X33 ^— X ^X>3

warunki dla odbiorców

i= 1

H4 + ^x24"b ^X34 S ^X'4

i=l

3

^X15+^X25+^X35 = Z ^XiS = ³⁰>

i=l

x_o.$s0 dla i =1,2,3;    7= 1,2,...,5,

K(Xy) = 503c₁₁+40x₁2 + 50x₁₃ + 20x₁4 + 5x₁₅ +

+ 40jc₂₁ + 80x₂₂ + 70x₂₃ + 30x₂₄ + 5x₂₅ +

+ 60x₃ i + 40x₃₂ + 70x₃₃ + 80x₃₄ + 6x₃₅    -> min.

97