Untitled Scanned 06 (16)

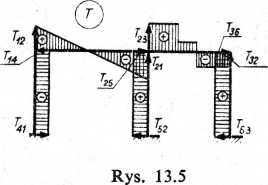
Wykres T rzeczywisty (wynikowy) dla elementu 1—2 (rys. 13.4a) sporządzimy, korzystając również z zasady superpozycji, sumując wykresy sił poprzecznych spowodowanych działaniem M_l2, M_2i, q i uwzględniając właściwe zwroty powyższych obciążeń. W punktach odpowiadających końcom pręta 1—2 pokazano właściwe dla rozpatrywanego przypadku zwroty reakcji, które odkładane od osi wykresu pokazują niejako automatycznie, z której strony należy odkładać dany-wykres sił poprzecznych. Na wykresie sumarycznym (rys. 13.4b) pokazane są wartości sił poprzecznych na podporach obliczone wg wzorów (13.5) i (13.6). Obliczenia dla następnych prętów ramy przeprowadzimy podobnie jak dla 1—2 i wykreślimy siły poprzeczne dla całości (rys. 13.5).

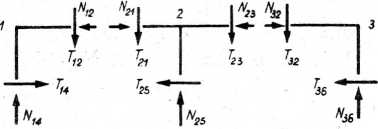
Rys. 13.6

Wykres ten możemy sporządzić również innym sposobem pamiętając, że siła poprzeczna jest pochodną momentu

(13.7)

dM dx ’

a geometrycznie przedstawia ona tangens kąta nachylenia stycznej do wykresu momentów zginających w danym punkcie (rys. 13.3):

(13.8)

T=tga.

Powyższą zależność wykorzystujemy m. in. do skontrolowania „na oko” prawidłowości końcowego wykresu sił poprzecznych drogą porównania go z końcowym wykresem momentów zginających.

Kontrolę prawidłowości znaków wykresu sił poprzecznych dla poszczególnych prętów można przeprowadzić stosując zasadę, że jeżeli wykres momentów kieruje się ku górze, wówczas siła poprzeczna jest ujemna, jeżeli zaś ku dołowi, siła poprzeczna jest dodatnia. Przebieg wykresu momentów rozpatrujemy dla każdego pręta, zakładając zwrot osi od lewego do prawego końca.

Na przykład patrząc na słup 1 — 4 od strony prawej widzimy, że idąc od lewego końca (węzeł 4) wykres M wznosi się ku górze, gdy natomiast patrzymy od lewej strony (węzeł 1), spostrzegamy, że wykres M również wznosi się ku górze. Znaczy to, że siła poprzeczna jest ujemna; znak T nie jest zależny od kierunku, z którego patrzymy na słup.

Aby określić siły podłużne (nprmalne), wycinamy kolejno węzły i układamy dla nich równania równowagi, rozpoczynając od tego węzła, w którym spotykają się jedynie dwa pręty (rys. 13.6).

Wytnijmy węzeł 1. Występują tu dwie siły poprzeczne: od rygla — siła T₁₂ i od słupa — siła r₁₄.

444