76353 Untitled Scanned 09 (16)

13.4.2. Kontrola wartości przemieszczeń

Po skontrolowaniu prawidłowości wykonania wykresów od obciążeń jednostkowych należy sprawdzić, czy nie popełniliśmy błędu przy obliczaniu wartości przemieszczeń 3ik-

Załóżmy, że obciążyliśmy układ podstawowy jednocześnie wszystkimi jednostkowymi wartościami niewiadomych nadliczbowych: X_t, X₂, X₃, ..., X„. Sporządźmy wykres momentów od tych obciążeń. Będziemy go nazywać sumarycznym wykresem jednostkowym.

Obciążenie takie wywoła przemieszczenie (Ą_s) punktu k w kierunku działania X_k pod wpływem działania na układ podstawowy wszystkich obciążeń jednostkowych:

<5fts = ^*1+^*2+Ąk3 + '"+$tt+”-+Ąbi*    (13.11)

Rzędne sumarycznego wykresu M_s równają się sumie rzędnych poszczególnych wykresów od obciążeń jednostkowych.

A więc:

M_s—M₁ + JWj+... + M_k +... + M„.    (13.12)

Przemieszczenie S_ks możemy określić jako

^ f M_kM_s

-JT^ds>    (13-13)

(przy założeniu pominięcia wpływu sił poprzecznych i podłużnych na odkształcenie).

Przyrównując do siebie prawe strony równania (13.11) i (13.13) oraz uwzględniając (13.12) otrzymamy:

<5*i+<5*2 + ---+^<5** + ---+<5_tol =

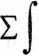
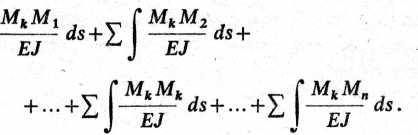
Lewa strona tego równania jest sumą współczynników przy niewiadomych w równaniu k, prawa zaś całką iloczynu momentów wykresu stanu X* = l i wykresu sumarycznego od obciążeń jednostkowych:

n

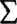
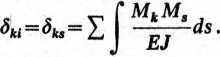
(13.14)

Suma przemieszczeń w dowolnym wierszu, w przypadku ramy utworzonej z prętów o stałych przekrojach, może być sprawdzona za pomocą sposobu Wereszczagina, tzn. drogą pomnożenia przez siebie odpowiednich pól i rzędnych wykresów momentów M_k oraz M_s i podzieleniu ich przez sztywności EJ. Jest to tzw. kontrola wierszowa.

447