21211 Untitled Scanned 09

- 18

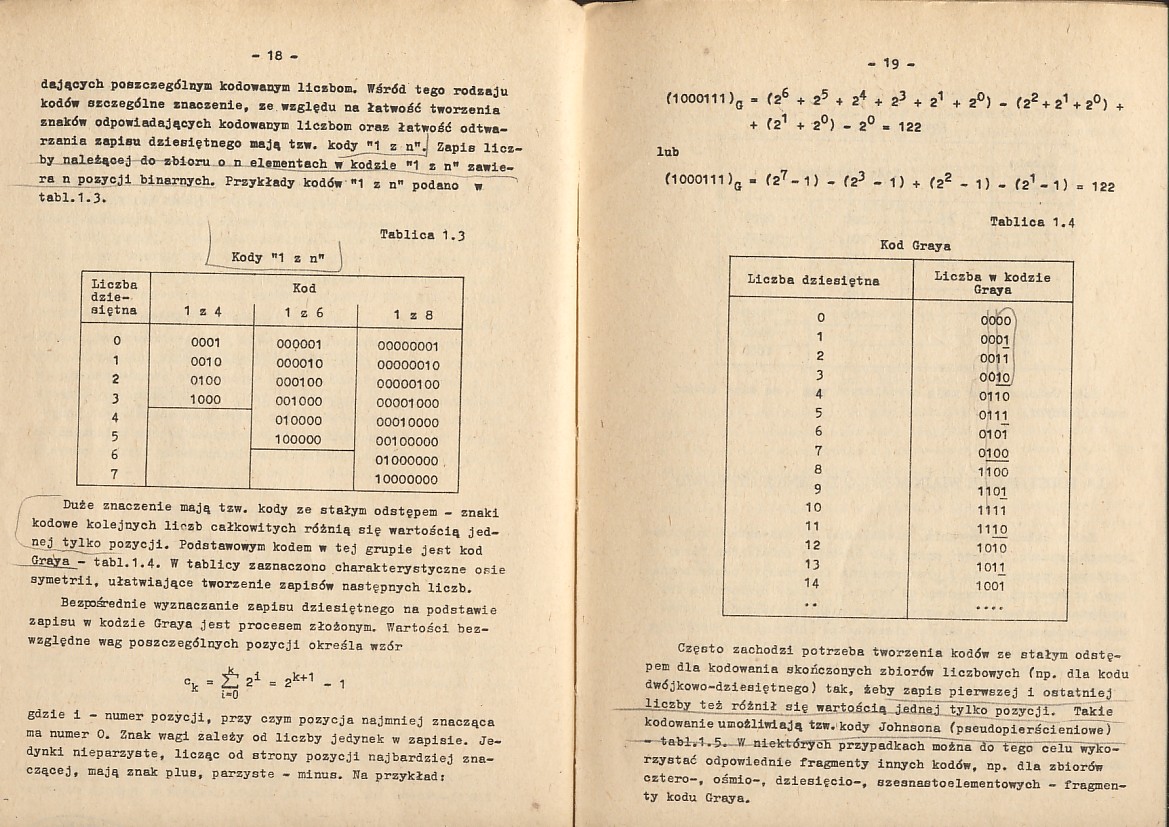
dających poszczególnym kodowanym liczbom. Wśród tego rodzaju kodów szczególne znaczenie, ze względu na łatwość tworzenia znaków odpowiadających kodowanym liczbom oraz łatwość odtwarzania zapisu dziesiętnego mają tzw. kody "1 z n"J Zapis liczby naleiąoej do zbioru o n elementach w^kodzie "1 z n" zawiera n pozycji binarnych. Przykłady kodów "1 z n" podano w tabl.1.3.

Tablica 1.3

Kody "1 z n"

Liczba dzie siętna	1 z 4	Kod 1 z 6	1 z 8
0	0001	000001	00000001
1	0010	000010	00000010
2	0100	000100	00000100
3	1000	001000	00001000
4		010000	00010000
5		100000	00100000
6			01000000
7			10000000

Duże znaczenie mają tzw. kody ze stałym odstępem - znaki kodowe kolejnych liczb całkowitych różnią się wartością jednej tylko pozycji. Podstawowym kodem w tej grupie jest kod _Graya - tabl.1.4. W tablicy zaznaczono charakterystyczne osie symetrii, ułatwiające tworzenie zapisów następnych liczb.

Bezpośrednie wyznaczanie zapisu dziesiętnego na podstawie zapisu w kodzie Graya jest procesem złożonym. Wartości bezwzględne wag poszczególnych pozycji określa wzór

C_k = £ 2¹ = 2^k+1 - 1

^K i-0

gdzie i - numer pozycji, przy czym pozycja najmniej znacząca ma numer 0. Znak wagi zależy od liczby jedynek w zapisie. Jedynki nieparzyste, licząc od Btrony pozycji najbardziej znaczącej, mają znak plus, parzyste - minus. Na przykład:

(1000111 )_Q » (2⁶ + 2⁵ + 2⁴ + 2³ + 2¹ + 2°) - (2² + 2¹ + 2°) + + (2¹ + 2°) - 2° - 122

lub

(1000111 )_Q - (2⁷ - 1 ) - (2³ - 1 ) + (2² - 1) - (2¹ - 1) = 122

Tablica 1.4

Kod Graya

Liczba dziesiętna	Liczba w kodzie Graya
0	66śo\
1	0001
2	0011
3	0010
4	0110
5	0111
6	0101
7	0100
8	1100
9	1101
10	1111
11	1110
12	1010
13	1012
14	1001
• •	0 0 0 9

Częnto zachodzi potrzeba tworzenia kodów ze otalym odstępem dla kodowania skończonych zbiorów liczbowych (np. dla kodu dwójkowo-dziesiętnego) tak, żeby zapis pierwszej i ostatniej liczby też różnił się wartością jednej tylko pozycji. Takie kodowanie umożliwiają tzw. kody Johnsona (pseudopierścieniowe)

- tabli-1.-5.--W niektórych przypadkach można do tego celu wykorzystać odpowiednie fragmenty innych kodów, np. dla zbiorów cztero-, ośraio-, dziesięcio-, ozesnastoolementowych - fragmenty kodu Graya.