MATEMATYKA159

308 VI. Ciqgi i szeregi funkcyjne

liml^-Jag, n-»« a_n

to promień zbieżności tego szeregu jest określony wzorem (3.1).

PRZYKŁAD 3.1. Znajdziemy zbiór tych x, dla których następujący szereg jest zbieżny:

b)£±x", c)£i(-ix)\ d)Z^"

Dla każdego z tych szeregów znajdziemy promień zbieżności r korzystając z twierdzenia 3.1 lub 3.2, a następnie zbadamy zbieżność szeregu dla x = ±r, gdy r jest liczbą różną od zera

a)    Ponieważ lim s/jaj = lim = -foo, więc r = 0. Szereg jest

nn~»w

więc zbieżny jedynie dla x = 0.

b)    Ponieważ limj^-Him, ⁿ-₁,_t=lim-~-=0, y\ięc r = +oc.

n-+-' a_n ^(n+1)! D-»n+l

Szereg jest więc zbieżny dla każdego x e R.

c)    Ponieważ lim 2/|aJ = lim "•—!—= yyięc r = 3. Oznacza

n~»<r *    n-+<r- y n ■ 3"    3

to, że szereg jest zbieżny dla xe(-3,3), a rozbieżny dla x e(-oo,-3)^(3,+oo). Zbadamy zbieżność tego szeregu dla x = 3 i dla

x = -3. Dla x = 3 otrzymujemy szereg £(-!)"— zbieżny (kryterium

n

Leibniza), a dla x = -3 otrzymujemy szereg £— rozbieżny (harmoniczny

n

rzędu a = 1). Zatem badany szereg jest zbieżny dla xe(-3,3>, a rozbieżny dla pozostałych x

tⁿ

d)    Przyjmijmy oznaczenie l-3x = t i rozważmy szereg p

2"n

Promień zbieżności tego szeregu jest równy r = 2, zatem szereg ten jest zbieżny dla t €(-2,2), a rozbieżny dla t e(-x,-2)w(2,+co). Dla t = 2

i dla t = -2 otrzymujemy szeregi zbieżne:    i £(-!)"—-. ^ak ^VV*S^C

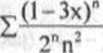
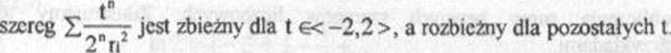
Ponieważ -2śt£2 <=> -2ś1 ~3x£2 o -l/3śx£l, więc badany

jest zbieżny dla x €<-1/3,1 >, a rozbieżny dla

pozostałych x.

WŁASNOŚCI SZEREGÓW POTĘGOWYCH. Załóżmy, że promieniem zbieżności szeregu £a_nxⁿ jest r > 0. Wówczas:

(1)    Szereg potęgowy jest Jednostajnie zbieżny na każdym przedziale domkniętym zawartym w przedziale zbieżności tego szeregu.

(2)    Suma szeregu potęgowego jest funkcją ciągłą na przedziale zbieżności.

(3)    Szereg potęgowy można różniczkować i całkować wyraz po wyrazie tzn. dla x £(-r,r)

(Z^an^X" ^{= S}(^X)) => (Z^nan^xn '^=S'(^X))>

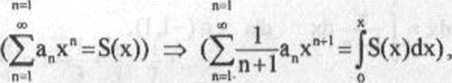
przy czym wszystkie szeregi wystęjmjące w tych wzorach mają ten sam promień zbieżności r.

(4) Jeżeli sumą szeregu potęgowego na przedziale (-r,r) jest S(x) i szereg ten jest zbieżny dla x = r. to suma tego szeregu dla x = r jest równa S(r-). Analogicznie: gdy szereg len Jest zbieżny dla x = -r , to suma tego szeregu dla x = -r Jest równa S(-r+).

Różniczkowanie i całkowanie szeregu potęgowego o znanej sumie może prowadzić do obliczenia sumy innych szeregów potęgowych, zaś różniczkowanie w odpowiednim punkcie lub całkowanie na odpowiednim przedziale szeregu potęgowego o znanej sumie może prowadzić do