new 99 (2)

202 7. Zasady obliczeń wytrzymałościowych śrub

202 7. Zasady obliczeń wytrzymałościowych śrub

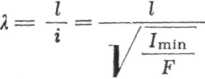
= 70,5.

720

/ 21935 / 210

Doraźną wytrzymałość na wyboczenie R_w dla smukłości / = 66 (10 < 1 < < Ź_k) obliczymy ze wzoru Tetmajera

J?_B =    = 310-1,19-70,5 = 226,5 MPa.

Ponieważ naprężenia ściskające a_c =—= - -—- = 34,3 MPa, stąd współ-

i* 210

czynnik bezpieczeństwa X_w = --- = —— 6,55.

CTC    uT)D

Otrzymaną wartość można uznać za zadowalającą.

Obliczenie nakrętki

Przyjmujemy, że nakrętka zostanie wykonana z brązu BA1032. Wysokość nakrętki A obliczymy z warunku nacisków na gwincie według wzoru (6.48)

Q

nd_st„n

Pdop*

Przyjmując zgodnie z tablicą 6.1 p_dop = 12 MPa, otrzymujemy

H = Pn :

PQ

2-7200 12

34,7 ~ 35 mm.

ndgt _np_dQp    7z -11 * 1 ■

Wymiary zewnętrzne nakrętki ze względu na współpracę z korpusem przyjmujemy konstrukcyjnie o przekroju kwadratowym 24X24.

Obliczenie przekładni zębatej

Moment obrotowy na kole czynnym (zębniku) jest równy momentowi korby. Zakładając siłę napędową na korbie P* = 30 N i jej ramię R = 180 mm, otrzymujemy wartość tego momentu

A!* = PR = 30 • 180 = 5400 N-mm.

Uwzględniając sprawność przekładni r\ = 0,9 obliczamy przełożenie przekładni

M_s ^    8525

M_kij    5400-0,9    ’ '

Zakładamy liczbę zębów zębnika Z\ — 12 stąd liczba zębów na kole biernym z₂ — zp. = 12-1,75 = 21. Kąt stożka podziałowego zębnika 0== z    12

= arc tg —— = arc tg ——— = 29 45'. z_;    21

Z obliczeń wytrzymałościowych (których tutaj nie zamieszczono) uzyskano średnie średnice kół Dj = 30,2 mm, D₂ = 52,8 mm oraz siły działające na zębnik: obwodową P₀ = 358 N, promieniową P_r=113 N oraz wzdłużną P_w = 66 N. W obliczeniu przyjęto, że koła będą wykonane z tworzywa sztucznego o nazwie handlowej „Tamoform”.

Obliczenie korby

Przyjęto, że korba wykonana zostanie z pręta o stałym przekroju ze stali St3, dla której można przyjąć dopuszczalne naprężenia zginające przy cyklu wahadłowym k_go — 50 MPa. Schemat obciążenia i założone wymiary korby przedstawiono na rys. 7.60.

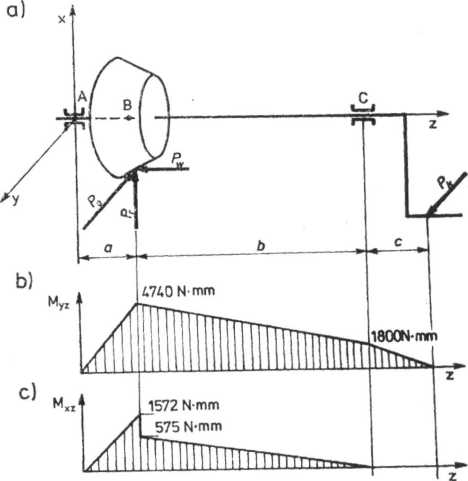
Rys. 7.60. Korba podnośnika: a) schemat obciążeń, b) wykres momentów gnących w płaszczyźnie yz, c) wykres momentów gnących w płaszczyźnie xz o = 15, b = 70, c = 60

Z równania równowagi momentów względem punktu A w płaszczyźnie yz mamy

£M_a = P_Da—P_C]/(a + b) — P_fc(a + b+c) = 0.

Obliczymy składową reakcję w punkcie C

„ P₀a-P_k{a+b + c)    358-15-30-145

tley — -|"T-=-—- = 12 IN

^v    a+b    85

oraz z równania SP„ = P₀— R_Au—R_cv—P_K = 0 składową reakcji w punkcie A

Ra_v = Po-Kc„-P_Ic = 358-12-30 = 316 N.