P1010285 (5)

Ogólne podstawy fotogrametrii

Załóżmy, te z dwóch punktów S| i S2. leżących na tej samej wysokości U terenem płaskim i poziomym, zostały wykonane dwa zdjęcia lotnicze ściśle pion©?

(rys. 21). Punkty A (wierzchołek drzewa) i C (leżący na tej samej wysokofa'*'Ś podstawa drzewa) odwzorowują się odpowiednio na zdjęciu 1 jako punkty z\ -,?*

- — ■ — - -    ~ - - mS » » —M    -• *    -•    ł ------J | | .

na zdjęciu 2 jako az i 02- Różnica wysokości między tymi punktami wy_no.;¹’

-------v n ---' ----------1---»--------------¹ h

(wysokość drzewa). Przyjmując prostą przechodzącą przez punkty Oi i O2 jal^ ⁿ odciętych (kierunek dodatni zgodny z kierunkiem wykonywania kolejnych yacf zaznaczmy za pomocą wektorów odległości interesujących nas punktów A i punktów głównych kolejnych zdjęć lotniczych. Otrzymamy odpowiednio weltt^

(V

(2)

A_2>

teren

77vW/;V

02A2

>iCt

A1A2

RYSUNEK 21. Zależność między przewyższeniem a różnicą paralaks podłużnych

O/Aj, OjC/, O2A2 i O2C2.

Uzupełniamy rysunek wektorem Aj A2. Możemy teraz napisać równanie we

rów:

(O1A2 — O2A2) - (0\C i- O2C2) = Ai A2

Jeżeli poszczególne wyrazy równania wektorów przemnożymy przez skali lotniczych, czyii przez f/H, wówczas równanie przyjmie postać:

fafl|-Xod-(xci-XcJ = A\Aljj

Różnicę odciętych punktu znajdującego się na dwóch kolejnych zdjęciach lotniczych tworzących stenogram nazywamy liniową paralaksą podłużną (p) punktu. Zatem równanie przyjmie postać:

Pa-Pc= MAljj

Lewą stroną równania jest różnica paralaks punktu A i C.

Oznaczając pa-pc- Ap otrzymamy:

Ap=A\A2^Jjj

Z podobieństwa trójkątów S1S2A i AA| A2 wynika że:

Bh

^MAl=n~r,

więc równanie przyjmuje postać:

(H-h)H

ale:

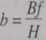
zatem równanie przyjmuje postać:

stąd:

. H . h = ~—-- Ap b+Ap

Wzór ten jest słuszny, jeżeli zdjęcia lotnicze tworzące stenogram są pionowe lub na takie zostały przetworzone i zostały wykonane z tej samej wysokości. Używając oryginalnych zdjęć lotniczych, trzeba się liczyć z tym, że wyznaczone ta drogą wysokości będą obarczone pewnymi błędami. Wielkości tych błędów uzaleźninft