P7240012

KAPITAŁ LUDZKI

NMOOOWAsnuntciA wOmoio

Publikacja wspólfinasowana przez Unią Europejską w ramach Europejskiego Funduszu Społecznego

BJRMM FUNOUSZ VCiK ZK»

4.4 Jak policzyć błąd pomiaru wykorzystując metodę (rozkład) Studenta? Praktyczny poradnik.

Uwaga! Jeśli chcesz wiedzieć dlaczego tak liczyć powinieneś przeczytać odpowiedni rozdział w książce poświęconej analizie danych doświadczalnych.

Przypuśćmy, że wykonałeś n pomiarów pewnej wielkości fizycznej w takich samych warunkach. Wyniki każdego pomiaru Xi są następujące:

*£ly    *£4?

Policz średnią (dodaj wszystkie i podziel przez liczbę wyników n)

yij-i Xj _ X\ + Xj + Xz + — + x_n n    n

(4.4.1)

Policz odchylenie standardowe S korzystając z wzoru

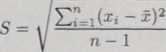
(4.4.2)

Oblicz błąd pomiaru Ax korzystając z wzoru

4^. — tf, _a .—

Vⁿ

(4.4.3)

biorąc odpowiedni współczynnik t_niCt z Tabeli 4.1,

Który współczynnik jest odpowiedni?

•    wybierz wiersz z odpowiednią ilością stopni swobody n — 1 (liczba twoich pomiarów minus jeden)

•    wybierz kolumnę z odpowiednim poziomem ufności a,

Które a jest odpowiednim a?

Na razie wybierz dowolne, na przykład a = 0.9 i czytaj dalej. Poniżej znajdziesz wyjaśnienie co znaczy a.

Policz błąd pomiaru Ar z wzoru (4.4.3) wykorzystując t_{n a} wybrane z tabeli a następnie zapisz wynik końcowy w postaci:

x = x ± Az

(4.4.4)

Co znaczy powyższy zapis?

Prawdopodobieństwo, że „prawdziwa" wartość mierzonej wielkości z jest większa niż i - Ar lecz mniejsza niż i -4- Ar wynosi a (Czyli w Twoim przypadku 0,9)

P(£ — Az < Ztrwc < X + A) = O

(4.4.5)

Jeżeli rozumiesz sens wyniku końcowego (równania (4.4.4) i (4.4.5)) wybór o powinien być łatwy, Tto wybór (wybór o) zależy od Ciebie. Zwykle wartości 0,9 lub 0,95 będą właściwe (Dlaczegct?),

Materiały pomocnicza do tek «iim<iinii»i'tyt.A t Fi*yjjf popracował ił.Knuabk, 9009)

33