PA275004

ANALIZA STATYSTYCZNA DANYCH

przy I stopniu swobody dla tego efektu i 54 stopniach swobody błędu (kolun^ DF) wynik testu F wynosi 35,70 (kolumna F) i jest on istotny statystycznie^ poziomie 0,001 (kolumna ISTOTNOŚĆ). Wynik ten zapisujemy w następujący sposób — F(1154) = 35,70; p < 0,001. Zapis ten jest analogiczny jak zapis jed% czynnikowej analizy wariancji. Z tego samego wiersza możemy też wyczytaćin. formacje na temat sumy kwadratów SS = 56,07 oraz średniego kwadratu MS ₅ 56,07, który można obliczyć dzieląc SS przez stopnie swobody. Przypomnijmy że średni kwadrat uzyskujemy dzieląc sumę kwadratów przez liczbę stopni swi. body dla danego efektu (MS = SS/dJ). Wynik testu F jest stosunkiem średniego kwadratu dla danego efektu (poszczególnych czynników oraz ich interakcji) i średniego kwadratu błędu, czyli wariancji wewnątrzgrupowej F = MS^/MS^ Informacji tych nie zamieszczamy jednak w raporcie z analiz.

Testy efektów międzyołHefctowycłł

Zmienna zależna- poczucie śzęzescja

Źródło zmienności	Typ III sumy kwadratów	df	Średni kwadrat	F	istotność
Model skorygowany	277,933*	5	55,587	35,387	.000
Stała	1251,267	1	1251,267	796,797	.000
zdrowie	56,067	1	56,067	35,703	,000
finanse	153.733	2	76,867	48,948	,000
zdrowie* finanse	68,133	2	34,067	21.693	,000
Błąd	84,800 I	54	1,570
Ogółem	1614,000	60
Ogółem skorygowane	362,733	59

3- R kwadrat= ,766 (Skorygowane R kwadrat = ,745)

Rys. 10.4. Statystyki F dla efektów głównych i efektu interakcji w dwuczynnikowej analizie wariancji.

Interpretacja efektu głównego czynnika ZDROWIE jest prosta, ponieważ był on mierzony na dwóch poziomach. W związku z tym, skoro uzyskaliśmy dla niego istotny statystycznie wynik testu F, to wiemy, że istnieje różnica w poziomie szczęścia osób, które charakteryzują się dobrym zdrowiem i tych, którym zdrowie nie dopisuje. Aby zrozumieć, która grupa cieszy się większym szczęściem, możemy spojrzeć na wykres średnich (rys. 10.5). Widzimy, że osoby o dobrym zdrowiu są bardziej szczęśliwe niż osoby o słabym zdrowiu.

Podobnie jak w przypadku efektu czynnika ZDROWIE zapiszemy wynik efektu głównego FINANSE, F(2, 54) — 48,95; p < 0,001, jak również wynik efektu interakcji, F(2, 54) = 21,69; p < 0,001 (por. tabela na rys. 10.4). Jednakże ich interpretacja jest trudniejsza, ponieważ porównujemy więcej niż dwie średnie. Istotny statystycznie wynik testu F mówi nam jedynie, że przynajmniej jedna średnia jest różna od pozostałych, ale nie wiemy która. Aby móc stwierdzić, że osoby z wysokimi zarobkami mają najwyższe poczucie szczęścia, osoby o średnim statusie finansowym niższe, a najniższe osoby o niskim statusie Finansowym, jak sugeruje to wykres na rys. 10.6, musimy przeprowadzić dodatkowe analizy, porównania średnich, post hoc lub analizę kontrastów.

10 • DWUCZYNNIKOWA ANAUZA WARIANCJI W SCHEMACIE...

Oszacowane średnie brzegowe - poczucie szczęścia

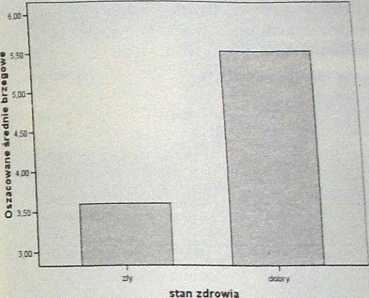
Rys. 10.5. Wykres średnich poczucia szczęścia ze względu na stan zdrowia uczestników badania.

Oszacowane średnie brzegowe - poczucie szczęścia

Rys. 10.6. Wykres średnich poczucia szczęścia ze względu no stan finansów uczestników badania.

Interpretacja efektu interakcji również jest niemożliwa jedynie na podstawie ogólnego wyniku testu F. Konieczny jest do niej dodatkowo zarówno wykres, jak i dalsze analizy' porównujące ze sobą poszczególne średnie. Ratrząc na wykres interakcji (por. rys. 10.7) widzimy, że osoby o dobrym zdrowiu cieszą się większym szczęściem, o ile również ich finanse są w bardzo dobrej lub średniej kondycji. Natomiast w sytuacji, kiedy status finansowy jest niski, osoby o słabym zdrowiu są