PC043346

Rozdział 3. Funkcje Jednej zmiennej

c) Ciąg (a„) określony warunkami

a i = 1, a„ = na„.\ dla n > 1

może być zapisany w postać

Definicja 3.2.

Ciąg (a„) spełniający warunek

MeR ne7V

nazywamy ciągiem ograniczonym.

Przykład 3.2.

Spośród ciągów z przykładu 3.1 ograniczone są jedynie dwa pierwsze.

Definicja 3.3.

Mówimy, że ciąg (a_n) jest:

a)    rosnący wtedy i tylko wtedy, gdy a„_+i > a_n dla każdego neN,

b)    malejący wtedy i tylko wtedy, gdy a_n+l < a„ dla każdego nzN,

c)    nierosnący wtedy i tylko wtedy, gdy a_n+l < a„ dla każdego neN,

d)    niemalejący wtedy i tylko wtedy, gdy a_n+i > a„ dla każdego neS. Ciąg mający przynajmniej jedną z wymienionych własności nazywamy cą. giem monofonicznym.

Przykład 3.3.

Zbadamy monotoniczność wybranych ciągów,

a) Ciąg a„ = n e N, jest monotoniczny. Istotnie,

a_n* i —a_n =

n + 1

2 (n+ 1)+ 1

Ciąg jest więc rosnący.

b) Ciąg a„ = (—1)'\ n € N, nie jest monotoniczny. Istotnie, łatwo zauważyć, it dh każdego n e JV mamy    = 2 > 0 oraz -«2« = —2 < 0. Różnice

mogą więc być różnych znaków, co wyklucza monotoniczność rozważanego dgi

Definicja 3.4.

Mówimy, że liczba g e R jest granicą ciągu (a_n) wtedy i tylko wtedy, gdy jest spełniony warunek

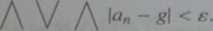
oO N,< R n>N,

(3.11

Fakt ten będziemy zapisywali w następujący sposób: a„ —» g lub lim a„ = f

fl $00

Jeśli ciąg ma granicę g, to mówimy także, że jest on ciągiem zbieżnym (do g).

matematyka

3.1. Ciągi liczbowe

Przykład 3.4.

a) Wykażemy, te ciąg a„ = ~, n e N. jest zbieżny do 0. Sprawdzimy, te jest spełniony warunek (3.1). Niech e > 0 będzie ustaloną liczbą. Mamy

n

e

Jeśli więc N_e > £, to warunek (3.1) będzie spełniony. Podobnie można pokazać, że np. lim jj* = 0.

b) Niech b będzie dowolną liczbą dodatnią. Jeśli n > log^ c, to

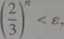
co oznacza, iż lim (1) =0.

H-łOO

c) Pokażemy, że ciąg a_n = (-1)", n ę N, nie ma granicy. Dokonamy tego metodą sprowadzania do sprzeczności. Załóżmy mianowicie, że pewna liczba g jest granicą tego ciągu. Z warunku (3.1) wynika, że dla wszystkich n > N, zachodzi nierówność I (-l)"-# l< £• Weźmy e = \. Jeśli n jest parzyste i n > N\p., to musi być spełniona nierówność |1 -g| < 4; jeśli zaś n jest nieparzyste i n > N\n, to |-1 -gi < 4- Jednak układ |l-gl<3.|l+gl<3 jest sprzeczny. Założenie o istnieniu granicy ciągu musiało więc być fałszywe. Dowód jest zakończony.

Twierdzenie 3.1.

Każdy ciąg ma co najwyżej jedną granicę.

Twierdzenie 3.2.

Jeżeli ciągi (a_n), (b_n) są zbieżne, odpowiednio, do liczb a, p, to

a) lim (a„ + b„) = a + /?,

b) lim a„b_n = ap, w szczególności lim (ca_n) = ca dla c € R.

c) lim f = g, gdy p # 0, b_n # 0.

W-KO    P

Przykład 3.5.

Wyznaczymy granice wybranych ciągów. Skorzystamy z przykładu 3.4 a) oraz b).

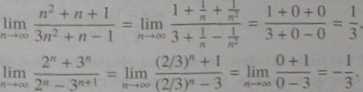
Rozważmy jeszcze ciąg a_n = Vn² + n - n. rt e /V. Przekształcenie jego wyrazów za pomocą tożsamości a² - b² = (a - b)(a + b) daje

n

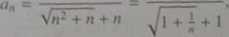
czyli granicą ciągu jest liczba i.