P3041014

5.16. Belki statycznie nlewyznaczalne

jako maksymalny (dla dźwigarów swobodnie podpartych w obrębie środka rozpiętości).

■    Moment zginający od obciążeń zmiennych, w każdym przęśle belki, może być zarówno dodatni jak też ujemny, co oznacza, że przy przewadze obciążeń zmiennych obydwa pasy belki mogą być ściskane. Projektując stężenie boczne belki przed zwichrzeniem, należy wtedy przewidzieć rozwiązania konstrukcyjne zabezpieczające oba pasy belki.

■    W przypadku konieczności projektowania żeber podłużnych, zabezpieczających środnik dźwigara przed niestatecznością miąjscową, należy umieszczać je na optymalnej wysokości środnika, bliżej pasa ściskanego.

■    Ugięcie przęseł belki ciągłej oblicza się w sposób uproszczony wg wzorów jak dla belki swobodnie podpartej ze współczynnikiem redukcyjnym, którego wartości zależą od rodząju obciążenia (stałe lub zmienne). Wartości tych współczynników podano w podrozdziale 2.6. W przypadku dowolnych obciążeń ugięcia oblicza się indywidualnie wg metod mechaniki budowli lub wzorów f9].

Zaprojektować dwuprzęsłowy stalowy spawany podciąg stropu, podparty w środku, a końcami na ścianie budynku. Długość obliczeniowa jednego przęsła równa się 12.24 m. Podciąg obciążony jest zastępczym równomiernie rozłożonym obciążeniem, pochodzącym od reakcji belek stropowych swobodnie podpartych rozstawionych co 2.04 m.

(

& Przykład 5.16

Rys.fi.G2

Obciążenie zawiera już ciężar własny podciągu. Pominąć obliczenia oparcia podciągu i konstrukcję żeber usztywniających środnik.

Materiał: stal St3SX.

Rozwiązanie

1. Obliczenie sił wewnętrznych Obliczenia przeprowadzono dla obciążeń obliczeniowych, korzystając z współczynników Winklera (9] przy wyznaczaniu momentów zginających. Rozpatrzono trzy warianty obciążeń zmiennych.

Wariant I

obciążenie stałe i zmienne na obu przęsłach (ry$.5.52a):

Me - 0,125 (30,35 + 67,8) 12.24² - 1838 khlm Vą - Vc • 0.375 (30,35 ♦ 67,8) 12,24 = 450.5 kN Ob do - (30,35 * 67,8) 0,625 12,24 = 750,9 kN Vb = 2 750.9 = 1501.8 kN

Maksymalny moment w przęśle A - B dla:

ilfiiiifa

wynosi:

Md = 0.5 450,5 4,59 = 1034 kNm

Podetowy proJeklowwrWa KoMCnUM# wni6*91*

Wariant II

P**yfc» obciążenie stałe na obu przęsła.....~r---------_T na przęśle ■ B

(rys5.52a):

A% - - 0,125 3036 12*4* - 0063 67A 12.24* - -566.4 6306 • 1206 kNm Va-05 96.15 12*4-    . 600.7 96.7-50? KN

Oh « 6007 ♦ 98 7 - 666.4 KN

06 = 0.5 30*6 12.24 *•    » 165.7 ♦ 96.7 • 264,4 KN

Vc-166.7-96.7-67* kN

Maksymalny moment w przęśle A - B (ta

v 502    .

**'99,15

wynosi: Me=0.5 902 5.11 * 1263 KNm Wariant III

Obciążanie stale na obu przęsłach, obaą*eme na przęśle B - C (rye652c) Wykorzystując obliczenia iak <*a wariantu II, przyjęto;

Mb 1200 KNm. Vą 87 KN. Oh - 264.4 KN. cC- 909.4 KN. V< 50S kN oraz maksimum momentu dki przęaaa A - B <fla

^X*⁼tH>.35 ^{= 2,87: Mr}‘°‘^{5 87} 287-125KNm

Wykresy obwiedni momentów i s«ł poprzecznych przedstawiono na rya.5 83 (96 części symetryczna) belki.

2. Zaprojektowanie przekroju poprzecznego dtwtgani

Przyjęto grubość środnika fW*9 mm

Wymagany wafcaZnśt wytrzymałości obsczymy z momemu przęaiowago. gdyś mo-mant podporowy obejmuje krótką stratę belki, czyi:

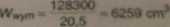
Wysokość środnika:

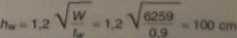
Przyjęto /W • 100 cm. Szerokość pasów:

przyjęto jako stalą na calsi Ugości dtwigara. Przewidziano zmianę grubości paaów w przekrojach jak na rya.S.53

Momenty zginające i sśy temafące db przyjętych przekrojów są U—tępjśąp* Mg- 502 3.40-03 96.15 3.4* * 1139 KNm Oq *506 -96.16 3.4 *502-334 • 166 kN AA = 450.5 11.4-03 96 15 11,40* -6136 6376- -1242 fcNm Ql - 4603 - 96.16 IM - -668 KN

Polo przokrefdw i grubość pasów oMezymy na podstawia maksymalnych wartości momentów zginających w poszczególnych przekrojach zgodnie ze wzorem