Scan Pic0050

Podobnie, z definicji natężenia pola grawitacyjnego

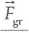
r-

m

można obliczyć wartość siły grawitacyjnej: F_gr = ym = 0,98-10"² N. Wypadkowa siła o wartości równej F_cl + F_gr nadaje kulce przyspieszenie o wartości

m

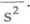
F.+F

—-Ł. = 9_x93

Rozwiązanie zadnia 3.18 Prawidłowa odpowiedź: A.

Pojemność kondenstaora równa jest z definicji

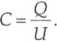
Dla próżniowego kondensatora płaskiego zależy ona od powierzchni S jego płytek i odległości d między nimi:

_{c =} fgS d

Porównanie obu wyrażeń na pojemność

Q _ ^£qS U~ d

U

d

równy wartości E natężenia pola (patrz

pozwala obliczyć stosunek

[3], str. 178,186):

_U_{=£ =} JL

d s_QS

Korzystając z definicji gęstości powierzchniowej ładunku

Q

S

mamy:

^£o

W zadaniu zakłada się, że kondensator jest odłączony od źródła napięcia, a więc gęstość ładunku na okładkach nie ulega zmianie (<7= const). Zmiana odległości między płytkami nie wywołuje więc zmiany natężenia pola: E = const.

Rozwiązanie zadnia 3.19 Prawidłowa odpowiedź: C.

Podobnie jak w poprzednim zadaniu, kondensator jest odłączony od źródła napięcia, więc jego ładunek nie ulega zmianie. Przeciwnie naładowane okładki przyciągają się wzajemnie i chcąc je oddalić musimy wykonać pracę. Wykonanie pracy spowoduje wzrost energii naładowanego kondensatora, czyli

AS=S₂-£₁=W.

Energię naładowanego kondensatora można wyrazić wzorem (patrz [3], str. 184):

Zgodnie z zależnością

C = io£ił d

trzykrotny wzrost odległości między okładkami zmniejszy trzykrotnie pojemność kondensatora. Początkową i końcową energię można zatem wyrazić następująco:

p _i QL ' i p ¹ o² 3 Q² 8i fc'    ² 2 ę 2 c '

3

Szukana praca wynosi zatem

Q²

Rozwiązanie zadnia 3.20

Prawidłowa odpowiedź: A.

Energia naładowanego kondensatora wyraża się wzorem:

P-AOL 2 C ■

Dwa kondenstaory połączone równolegle można zastąpić jednym o dwukrotnie większej pojemności (patrz [3], str. 182). Ładunek Q pozostaje taki sam, więc energia zmaleje dwukrotnie.

- 99 -