Scan Pic0089

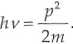
Zgodnie z teorią Einsteina (por. z zad. 6.11) pęd p_f fotonu jest równy

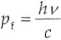
Podstawiając obliczoną wyżej energię h y fotonu otrzymujemy

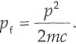
Rozwiązanie zadania 6.13 Prawidłowa odpowiedź: D.

Zgodnie z informacjami podanymi w zadaniu 6.8 zachodzi równość hv_ma = h——— = ell.

max    *

^/tmin

Stąd pęd fotonu odpowiadający krótkofalowej granicy widma wynosi

c c

Rozwiązanie zadania 6.14 Prawidłowa odpowiedź: D.

Stała Plancka występuje we wzorach na energię E = hv i pęd p = —— = —

c ŹL

fotonu. Z tych wzorów wynika, że stała ta nie może mieć wymiaru ani pędu, ani energii, ani częstotliwości. Sprawdźmy zatem, czy ma ona wymiar momentu pędu b:

«3- II	stąd	[&] = lkg^ s
II	stąd	[h] = lkg^ s

Rozwiązanie zadania 6.15

Prawidłowa odpowiedź: D.

Natężenie wiązki promieniowania X po przejściu przez osłonę o grubości d ulega zmniejszeniu. Zjawisko to opisuje zależność

I = 1 p~»^d *’³¹0^c /

gdzieI₀ jest natężeniem wiązki padającej,! - natężeniem wiązki po przejściu przez osłonę, a fi jest współczynnikiem absorpcji zależnym od liczby atomowej Z materiału osłony i rośnie wraz ze wzrostem Z.

Rozwiązanie zadania 6.16 Prawidłowa odpowiedź: D.

Długość fali odpowiadająca maksimum natężenia promieniowania ciała doskonale czarnego jest odwrotnie proporcjonalna do temperatury:

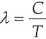
gdzie C jest współczynnikiem proporcjonalności. W temperaturze T,^mT mamy

mamy

W temperaturze T₂=T + -^-T = -^-T

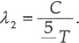
4

Dzieląc stronami powyższe równania otrzymujemy:

IgŁ—stąd M? = — /L. %    5 ^ą 2    5 ¹

A zatem

/L -X. = -X_r-X₁

^{2    1}    ₅ i i ₅ i

Rozwiązanie zadania 6.17 Prawidłowa odpowiedź: D.

W modelu Bohra budowy atomu wodoru energia elektronu na n-tej orbicie jest dana wyrażeniem (patrz [2], str. 24):

Na pierwszej orbicie elektron ma więc energię o wartości podanej w temacie zadania E₁ = - 13,6 eV. Na trzeciej orbicie energia elektronu jest

E, ,= -riM-_eV = -l-£ _eV > E,.

3    ₉    1

- 177 -